Solved Examples and Worksheet for Interpreting Box Plots and Finding Interquartile Range
Step: 1
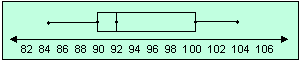
In a box and whisker plot outlier is the data value that should be less than the [lower quartile - (1.5 x IQR)] or greater than the [upper quartile + (1.5 x IQR)].
Step: 2
IQR = upper quartile - lower quartile
= 100 - 90 = 10
[upper quartile = 100 and lower quartile = 90.]
Step: 3
Lower quartile - (1.5 x IQR) = 90 - (1.5 x 10) = 75
[Substitute and subtract.]
Step: 4
Upper quartile + (1.5 x IQR) = 100 + (1.5 x 10) = 115
[Substitute and simplify.]
Step: 5
In the box and whisker plot all the values are between 82 and 106. So, there is no value less than 75 or greater than 115.
Step: 6
So, in the data there is no outlier.
Correct Answer is : No outlier
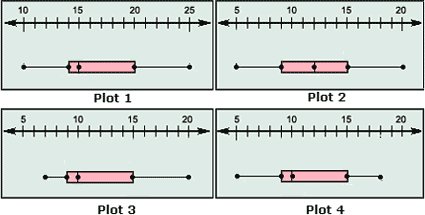
A. Plot 1
B. Plot 2
C. Plot 3
D. Plot 4
Step: 1
The number of customers who visited the super market each hour are 15, 10, 12, 9, 18, 5, 8, 9, 15, 10 and 11.
Step: 2
The ascending order of the above data set is: 5, 8, 9, 9, 10, 10, 11, 12, 15, 15,18.
Step: 3
The least value in the above list of data is 5 and the greatest value is 18.
Step: 4
Middle quartile = median of the data = 10.
Step: 5
Lower quartile = median of lower half of the data = 9.
Step: 6
Upper quartile = median of upper half of the data = 15.
Step: 7
So, among the plots, plot 4 is the equivalent box-and-whisker plot for the data.
Correct Answer is : Plot 4
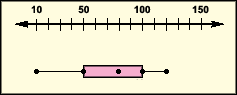
A. 80 miles/ hour
B. 50 miles/ hour
C. 10 miles/ hour
D. 100 miles/ hour
Step: 1
Median of a given data is equal to the middle quartile value in its equivalent box-and-whisker plot.
Step: 2
From the box-and-whisker plot, the middle quartile value = 80.
Step: 3
So, the median speed of the car = 80 miles/ hour.
Correct Answer is : 80 miles/ hour
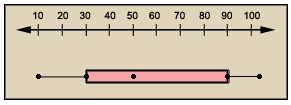
A. 40
B. 50
C. 10
D. 80
Step: 1
From the box-and-whisker plot, least value = 10 and middle quartile = 50.
Step: 2
The difference between the middle quartile and the least value = middle quartile - least value
= 50 - 10
= 40
= 40
Correct Answer is : 40
Step: 1
From the box and whisker plot, lower quartile is 7 and upper quartile is 11.
[Lower quartile is the median of the lower half and upper quartile is the median of the upper half of data set.]
Step: 2
Outlier for the box and whisker plot is the value less than (lower quartile- 1.5 x IQR) or the value greater than (upper Quartile +1.5 x IQR).
[IQR = inter quartile range = upper quartile - lower quartile.]
Step: 3
IQR for the box and whisker plot = 11 - 7 = 4
[Subtract lower quartile value from upper quartile value.]
Step: 4
(Lower Quartile - 1.5 x IQR) = 7 - 1.5 x 4 = 7 - 6 = 1
Step: 5
Upper Quartile + 1.5 x IQR = 11 + 1.5 x 4 = 11 + 6 = 17
Step: 6
For being the outlier, the data value must be less than 1 or greater than 17.
Step: 7
There is no such value in the plot as the least value of the plot is 5 and the highest value is 16.
Step: 8
So, there is no outlier for the box and whisker plot.
Correct Answer is : No outlier
A. 17
B. 14
C. 8
D. 30
Step: 1
The ascending order of the above data set is 8, 10, 12, 13, 14, 17, 17, 21, 23, 28, 30.
Step: 2
The middle quartile = Median of the entire data set = 17
Correct Answer is : 17
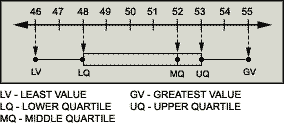
A. 48
B. 46
C. 53
D. 52
Step: 1
The lower quartile is the median of the data values from the least value to the middle quartile.
Step: 2
The box in a box-and-whisker plot always starts from the lower quartile value.
Step: 3
The lower quartile of the box-and-whisker plot = 48.
Correct Answer is : 48
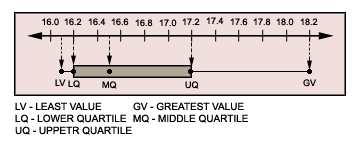
A. 2.1
B. 1.5
C. 4.5
D. 2.5
Step: 1
From the box-and-whisker plot, the greatest value is 18.2 and the least value is 16.1
Step: 2
Range = Greatest value - Least value
Step: 3
Range of the given data = 18.2 - 16.1 = 2.1
[Subtract.]
Correct Answer is : 2.1
A. 20.5
B. 22.5
C. 40
D. 20
Step: 1
The interquartile range is the difference between the upper quartile and the lower quartile.
Step: 2
Arrange the given data in ascending order
25, 25, 30, 35, 40, 40, 40, 50, 50, 75
25, 25, 30, 35, 40, 40, 40, 50, 50, 75
Step: 3
Lower quartile = 30
Upper quartile = 50
Upper quartile = 50
Step: 4
Interquartile range = upper quartile - lower quartile
= 50 - 30 = 20
Step: 5
So, the interquartile range for the given data is 20.
Correct Answer is : 20
A. 13.5
B. 6.5
C. 9
D. 20
Step: 1
Interquartile range is the difference between the upper quartile and the lower quartile.
Step: 2
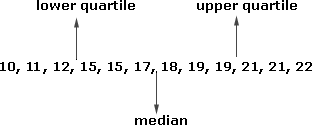
Step: 3
Interquartile range = upper quartile - lower quartile
= 21 - 13.5 =
6.5
Step: 4
So, the interquartile range of the scores given is 6.5.
Correct Answer is : 6.5
A. 6
B. 15
C. 10
D. 9
Step: 1
The interquartile range is the difference between the upper quartile and the lower quartile.
Step: 2
Arrange the given data in ascending order
2,3,5,8,9,9,10,10,11,12,13
2,3,5,8,9,9,10,10,11,12,13
Step: 3
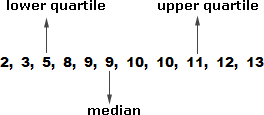
Step: 4
Lower quartile = 5
Upper quartile = 11
Upper quartile = 11
Step: 5
Interquartile range = upper quartile - lower quartile
= 11 - 5 = 6
Step: 6
So, the interquartile range for the given data is 6.
Correct Answer is : 6
A. 4
B. 3.5
C. 5
D. 7.5
Step: 1
Interquartile range is the difference between upper quartile and lower quartile of a data set.
Step: 2
Label lower and upper quartiles in the given figure as shown below.
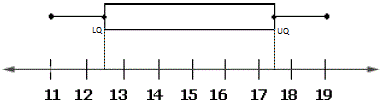

Step: 3
Upper quartile in the above figure = 12.5.
Lower quartile in the above figure = 17.5.
Lower quartile in the above figure = 17.5.
Step: 4
Interquartile range = upper quartile - lower quartile
Step: 5
= 17.5 - 12.5
[From step 3.]
Step: 6
= 5
[Subtract.]
Step: 7
Therefore, interquartile range in the given figure is 5.
Correct Answer is : 5
A. Ask his friends.
B. Select a few grades, and ask few students in each grade.
C. Ask all the teachers in the school.
Step: 1
A sample is a part of the population.
Step: 2
In a random sample, each object in the population has an equal chance of being selected.
Step: 3
Selecting few grades and asking few students is random sampling.
Step: 4
So, the best sampling method used by Micky is 'Select a few grades, and ask few students in each grade'.
Correct Answer is : Select a few grades, and ask few students in each grade.
- Collecting Data-Formulating a Question-Gr 6-Solved Examples
- Measures of Central Tendency-Gr 6-Solved Examples
- Measures of Central Tendency-Gr 6-Solved Examples
- Appropriate Measures of Central Tendency for the Data-Gr 6-Solved Examples
- Range-Gr 6-Solved Examples
- Interpreting Histograms-Gr 6-Solved Examples
- Interpreting Line Plots-Gr 6-Solved Examples
- Interpreting Scatter Plots-Gr 6-Solved Examples
Related Worksheet
- Data
- Range (Of Data)