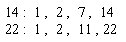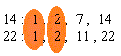Solved Examples and Worksheet for Greatest Common Factors of Whole Numbers
Step: 1
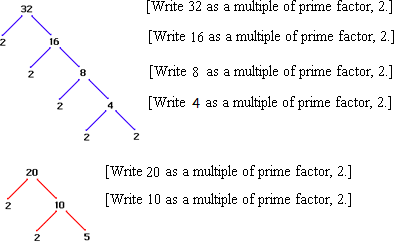
Draw a factor tree for each number.

Step: 2
20 = 5 × 2 × 2
32 = 2 × 2 × 2 × 2 × 2
32 = 2 × 2 × 2 × 2 × 2
[Write the prime factorization for each number.]
Step: 3
Identify the common factors.
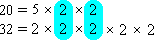
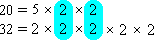
Step: 4
2 × 2 = 4
[Multiply the common factors.]
Step: 5
The GCF of 20 and 32 is 4.
Correct Answer is : 4
Step: 1
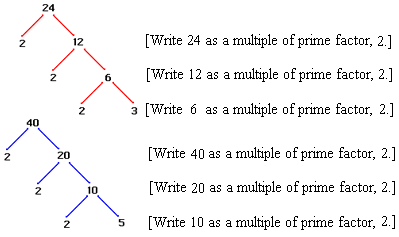
Draw a factor tree for each number.

Step: 2
24 = 3 × 2 × 2 × 2
40 = 5 × 2 × 2 × 2
40 = 5 × 2 × 2 × 2
[Write the prime factorization for each number.]
Step: 3
[Identify the common factors.]
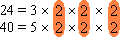
Step: 4
2 × 2 × 2 = 8
[Multiply the common factors.]
Step: 5
The GCF of 24 and 40 is 8.
Correct Answer is : 8
A. 5 and 20
B. 10 and 15
C. 5 and 10
D. 5 and 12
Step: 1
If a number is the GCF of any two numbers, then the two numbers are multiples of that GCF.
Step: 2
1 x 5 = 5
2 x 5 = 10
2 x 5 = 10
[Write the first two multiples of 5.]
Step: 3
The two smallest numbers whose GCF is 5 are 5 and 10.
Correct Answer is : 5 and 10
Step: 1
The prime factorisation of 72 and 84 are:
72 = 23 × 32
84 = 22 × 3 × 7
72 = 23 × 32
84 = 22 × 3 × 7
Step: 2
H.C.F. is found by multiplying all the prime factors having the least powers.
Step: 3
Therefore, the H.C.F. of 72 and 84 = 22 × 3 = 12.
Correct Answer is : 12
Step: 1
While using Long Division Method for finding H.C.F. of two numbers, follow these steps:
(1) Divide the larger number by the smaller number.
(2) Divide the divisor by the remainder.
(3) Repeat the process of dividing until you get remainder as 0. The divisor which gives remainder 0 is the H.C.F.
(1) Divide the larger number by the smaller number.
(2) Divide the divisor by the remainder.
(3) Repeat the process of dividing until you get remainder as 0. The divisor which gives remainder 0 is the H.C.F.
Step: 2
Using the long division method, we get the H.C.F. of 1824 and 2304 as follows:
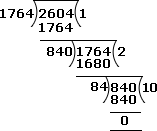
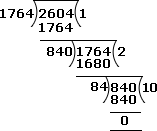
Step: 3
In the division above, the divisor 84 gives remainder 0. Therefore, the H.C.F. of 1764 and 2604 is 84.
Correct Answer is : 84
Step: 1
H.C.F. of three numbers = H.C.F. of [(H.C.F. of any two) and the third.]
Step: 2
First we find the H.C.F. of any two of the given numbers.
Step: 3
While using Long Division Method for finding H.C.F. of two numbers, follow these steps:
(1) Divide the larger number by the smaller number.
(2) Divide the divisor by the remainder.
(3) Repeat the process of dividing until you get remainder as 0. The divisor which gives remainder 0 is the H.C.F.
(1) Divide the larger number by the smaller number.
(2) Divide the divisor by the remainder.
(3) Repeat the process of dividing until you get remainder as 0. The divisor which gives remainder 0 is the H.C.F.
Step: 4
First, let us find the H.C.F. of 714 and1666. Using the long division method, we get the H.C.F. of 714 and 1666 as follows:
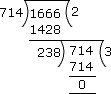
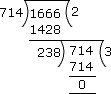
Step: 5
In the division above, the divisor 238 gives remainder 0. Therefore, the H.C.F. of 714 and 1666 is 238.
Step: 6
Repeat the same process for the remaining number and the divisor 238 which got the remainder as 0.
Step: 7
Using the long division method, we get the H.C.F. of 238 and 9775 as follows:
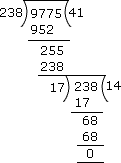
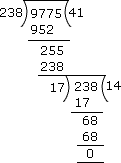
Step: 8
In the division above, the divisor 17 gives remainder 0. Therefore, the H.C.F. of 238 and 9775 is 17.
Step: 9
Hence, the H.C.F. of 714, 1666 and 9775 is 17.
Correct Answer is : 17
Step: 1
The prime factorisation of 630, 576 and 1080 are:
630 = 2 × 32 × 5 × 7
576 = 26 × 32
1080 = 23 × 33 × 5
630 = 2 × 32 × 5 × 7
576 = 26 × 32
1080 = 23 × 33 × 5
Step: 2
H.C.F. is found by multiplying all the prime factors having the least powers.
Step: 3
Therefore, the H.C.F. of 630, 576 and 1080 = 2 × 32 = (2 × 9) = 18.
Correct Answer is : 18
Step: 1
The prime factorisation of 1965, 1755 and 1560 are:
1965 = 3 × 5 × 131
1755 = 33 × 5 × 13
1560 = 23 × 3 × 5 × 13
1965 = 3 × 5 × 131
1755 = 33 × 5 × 13
1560 = 23 × 3 × 5 × 13
Step: 2
H.C.F. is found by multiplying all the prime factors having the least powers.
Step: 3
Therefore, the H.C.F. of 1965, 1755 and 1560 = 3 × 5 = 15.
Correct Answer is : 15
Step: 1
The prime factorisation of 972 and 432 are:
972 = 22 × 35
432 = 24 × 33
972 = 22 × 35
432 = 24 × 33
Step: 2
H.C.F. is found by multiplying all the prime factors having the least powers.
Step: 3
Therefore, the H.C.F. of 972 and 432. = 22 × 33 = (4 × 27) = 108.
Correct Answer is : 108
Step: 1
List all the factors of the numbers.
Factors of 7: 1 and 7
Factors of 21: 1, 3, 7 and 21
Factors of 7: 1 and 7
Factors of 21: 1, 3, 7 and 21
Step: 2
Select the common factors.
Factors of 7: 1 and 7
Factors of 21: 1, 3, 7 and 21
Factors of 7: 1 and 7
Factors of 21: 1, 3, 7 and 21
Step: 3
Among the common factors 1 and 7, the greatest common factor is 7.
Step: 4
Therefore, the greatest common factor of 7 and 21 is 7.
Correct Answer is : 7
Step: 1
List all the factors of the numbers.
Factors of 40: 1, 2, 4, 5, 8, 10, 20 and 40
Factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48.
Factors of 40: 1, 2, 4, 5, 8, 10, 20 and 40
Factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48.
Step: 2
Select the common factors.
Factors of 40: 1, 2, 4, 5, 8, 10, 20 and 40.
Factors of 48: 1, 2, 4, 6, 8, 12, 16, 24 and 48
Factors of 40: 1, 2, 4, 5, 8, 10, 20 and 40.
Factors of 48: 1, 2, 4, 6, 8, 12, 16, 24 and 48
Step: 3
Among the common factors 1, 2, 4 and 8, the greatest common factor is 8.
Step: 4
Therefore, the greatest common factor of 40 and 48 is 8.
Correct Answer is : 8
A. 8 and 16
B. 1 and 8
C. 16 and 24
D. 16 and 20
Step: 1
Multiplying 1 and 8, we get the value as 8.
[The smallest number is 1 and the GCF is 8.]
Step: 2
Multiplying 2 and 8, we get the value as 16.
[The second smallest number is 2 and the GCF is 8.]
Step: 3
8 = 1, 8
16 = 1, 2, 8, 16
16 = 1, 2, 8, 16
[Write the factors for the two values 8 and 16.]
Step: 4
Select the common factors.
Step: 5
8 and 16 are the two smallest possible numbers with GCF 8.
Correct Answer is : 8 and 16
- Locating Integers on a Number Line-Gr 6-Solved Examples
- Application of Division of Whole Numbers-Gr 6-Solved Examples
- Application of Integers-Gr 6-Solved Examples
- Dividing Fractions with/without Models-Gr 6-Solved Examples
- Operations on Decimals-Gr 6-Solved Examples
- Least Common Multiples of Whole Numbers-Gr 6-Solved Examples
- Finding Absolutes Value of Rational Numbers-Gr 6-Solved Examples
- Identifying or Locating Ordered Pairs on a Coordinate Plane-Gr 6-Solved Examples
- Counting Distance on a Horizontal or Vertical Line-Gr 6-Solved Examples
Related Worksheet
- Whole Numbers