Solved Examples and Worksheet for Volumes of Composite 3-D Shapes

Q1Find the volume of composite 3-D shape.

A. 2 100 cm3
B. 800 cm3
C. 1 800 cm3
D. 1 900 cm3

Solutions
Share 
Step: 1
The volume of the composite 3-D shape can be found by finding the volume of the individual shapes and adding them up.
Step: 2
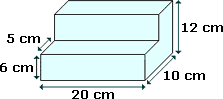
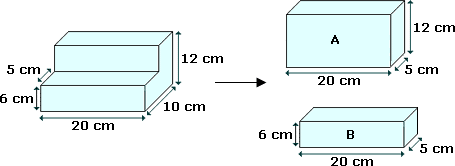
The given composite shape is divided into two cuboids as shown.
Step: 3
Volume of the cuboid = Length × width × Height
Step: 4
Volume of cuboid A = 20 cm × 5 cm × 12 cm = 1 200 cm3
  [Length = 20 cm, width = 5 cm and Height = 12 cm]
Step: 5
Volume of cuboid B = 20 cm × 5 cm × 6 cm = 600 cm3
  [Length = 20 cm, width = 5 cm and Height = 6 cm]
Step: 6
Total volume = 1 200 cm3 + 600 cm 3 = 1 800 cm3
  [Total volume = Volume of the cuboid A + Volume of the cuboid B]
Step: 7
The volume of the composite 3-D shape is 1 800 cm3.
Correct Answer is :   1 800 cm3
Q2Find the volume of the compsite 3-D shape.


A. 278 cm3
B. 280 cm3
C. 270 cm3
D. 280 cm2

Solutions
Share 
Step: 1
The volume of the composite 3-D shape can be found by finding the volume of the individual shapes and adding them up.
Step: 2
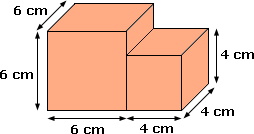
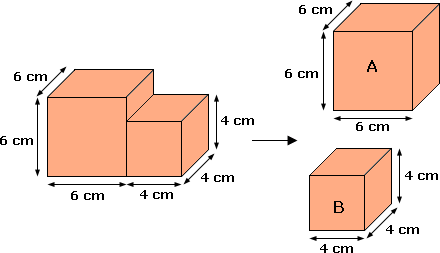
The given composite shape is divided into two cubes as shown.
Step: 3
Volume of the cube = Length × width × Height
Step: 4
Volume of cube A = 6 cm × 6 cm × 6 cm = 216 cm3
  [Length = 6 cm, width = 6 cm and Height = 6 cm]
Step: 5
Volume of cube B = 4 cm × 4 cm × 4 cm = 64 cm3
  [Length = 4 cm, width = 4 cm and Height = 4 cm]
Step: 6
Total volume = 216 cm3 + 64 cm3 = 280 cm3
  [Total volume = Volume of cube A + Volume of cube B]
Step: 7
The volume of the composite 3-D shape is 280 cm3.
Correct Answer is :   280 cm3
Q3Find the volume of the compsite 3-D shape.

A. 80 cm3
B. 81 cm3
C. 78 cm3
D. 88 cm3

Solutions
Share 
Step: 1
The volume of the composite 3-D shape can be found by finding the volume of the individual shapes and adding them up.
Step: 2
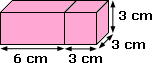
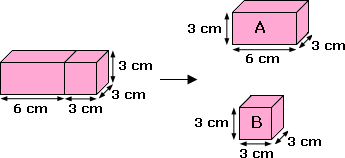
The given composite shape is divided into a cuboid and a cube as shown.
Step: 3
Volume = Length × width × Height
Step: 4
Volume of A = 6 cm × 3 cm × 3 cm = 54 cm3
  [Length = 6 cm, width = 3 cm and Height = 3 cm]
Step: 5
Volume of B = 3 cm × 3 cm × 3 cm = 27 cm3
  [Length = 3 cm, width = 3 cm and Height = 3 cm]
Step: 6
Total volume = 54 cm3 + 27 cm3 = 81 cm3
  [Total volume = Volume of A + Volume of B]
Step: 7
The volume of the composite 3-D shape is 81 cm3.
Correct Answer is :   81 cm3
Q4The diagram shows the combination of two identical cubes and a cuboid. Find the volume of the solid, in cm3.


A. 375 cm3
B. 250 cm3
C. 425 cm3
D. 450 cm3

Solutions
Share 
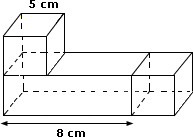
Step: 1
Volume of the cube = length × length × length
= 5 cm × 5 cm × 5 cm
= 125 cm3
  [Substitute the value and multiply.]
Step: 2
Volume of two such cubes = 2 × Volume of the cube
= 2 × 125 cm3
= 250 cm3
  [Substitute the value and multiply.]
Step: 3
Volume of the cuboid = length × width × height
= 8 cm × 5 cm × 5 cm
= 200 cm3
  [Multiply.]
Step: 4
Volume of the given solid = Volume of the two cubes + Volume of the cuboid
= 250 cm3 + 200 cm3
= 450 cm3
Step: 5
So, the volume of the given solid is 450 cm3.
Correct Answer is :   450 cm3
Q5The diagram shows the combination of a cube and a cuboid. The volume of the cuboid is 3 times the volume of the cube. Find the volume of the cuboid in cm3.

A. 105 cm3
B. 125 cm3
C. 375 cm3
D. 365 cm3

Solutions
Share 
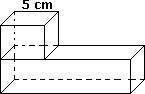
Step: 1
Volume of the cube = length × length × length = 5 cm × 5 cm × 5 cm
  [Multiply.]
Step: 2
= 125 cm3
Step: 3
Volume of the cuboid = 3 × Volume of the cube
= 3 × 125 cm3
= 375 cm3
  [Multiply.]
Step: 4
So, the volume of the cuboid is 375 cm3.
Correct Answer is :   375 cm3
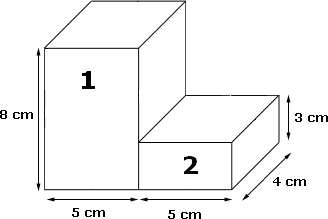
Q6Two wooden blocks are arranged as shown in the figure. Find the combined volume of the blocks.


A. 200 cm3
B. 220 cm3
C. 160 cm3
D. 120 cm3

Solutions
Share 
Step: 1
Volume of block 1 = Length × width × Height = 5 cm × 4 cm × 8 cm = 160 cm3
Step: 2
Volume of block 2 = Length × width × Height = 5 cm × 4 cm × 3 cm = 60 cm3
Step: 3
Total volume = 160 cm3 + 60 cm3 = 220 cm3
Step: 4
The combined volume of the blocks is 220 cm3.
Correct Answer is :   220 cm3
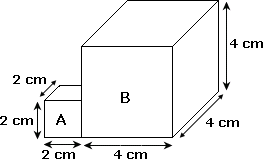
Q7Two cubic iron blocks are arranged as shown in the figure. Find the combined volume of the iron blocks.

A. 18 cm3
B. 72 cm
C. 18 cm
D. 72 cm3

Solutions
Share 
Step: 1
Volume of an iron block A = Length × width × Height = 2 cm × 2 cm × 2 cm = 8 cm3
Step: 2
Volume of an iron block B = Length × width × Height = 4 cm × 4 cm × 4 cm = 64 cm3
Step: 3
Total volume = 8 cm3 + 64 cm3
= 72 cm3
Step: 4
The combined volume of the iron blocks is 72 cm.3
Correct Answer is :   72 cm3
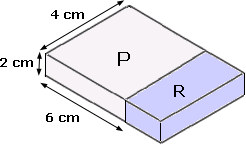
Q8The diagram shown is the overview of a building. Volume of R is half the volume of P. Find the total volume of the figure.

A. 82 cm3
B. 144 cm3
C. 72 cm3
D. 76 cm3

Solutions
Share 
Step: 1
Volume of P = Length × width × Height = 6 cm × 4 cm × 2 cm = 48 cm3
Step: 2
Volume of R = 12 × 48 cm3 = 24 cm3
Step: 3
Total volume of the figure = 48 cm3 + 24 cm3 = 72 cm3
Step: 4
The total volume of the figure is 72 cm3.
Correct Answer is :   72 cm3
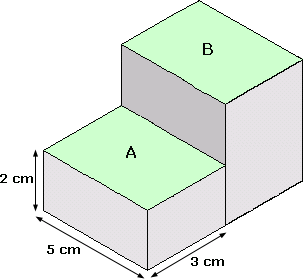
Q9The diagram shows 2 uneven blocks arranged in a row. The figure has 2 cuboids A and B. The volume of B is 2 times that of the volume of A. Find the total volume of the figure.


A. 15 cm3
B. 60 cm3
C. 45 cm3
D. 90 cm3

Solutions
Share 
Step: 1
Volume of A = Length × width × Height = 5 cm × 3 cm × 2 cm = 30 cm3
Step: 2
Volume of B = 2 × Volume of A
Step: 3
= 2 × 30 cm3 = 60 cm3
Step: 4
Total volume of the figure = 30 cm3 + 60 cm3 = 90 cm3
Step: 5
The total volume of the figure is 90 cm3.
Correct Answer is :   90 cm3
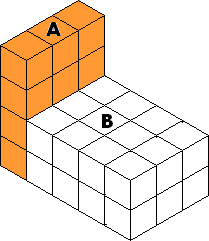
Q10Find the volume of the composite 3-D shape shown, where each small cube measures 1 m3.


A. 28 m3
B. 32 m3
C. 21 m3
D. 36 m3

Solutions
Share 
Step: 1
To find the volume of the composite 3-D shape, count the number of small cubes in both A and B and add.
Step: 2
Number of small cubes filled in cuboid A is 12.
  [Count the number of small cubes in cuboid A.]
Step: 3
Volume of A = 12 × 1 m3 = 12 m3
Step: 4
Number of small cubes filled in cuboid B is 24.
  [Count the number of small cubes in cuboid B.]
Step: 5
Volume of B = 24 × 1 m3 = 24 m3
Step: 6
Total volume = Volume of A + Volume of B = 12 m3 + 24 m3 = 36 m3
Step: 7
Volume of the composite 3-D shape is 36 m3.
Correct Answer is :   36 m3
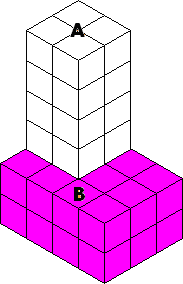
Q11Find the volume of the composite 3-D shape shown, where each small cube measures 1 m3.

A. 44 m3
B. 38 m3
C. 40 m3
D. 28 m3

Solutions
Share 
Step: 1
To find the volume of the composite 3-D shape, count the number of small cubes in both A and B and add.
Step: 2
Number of small cubes filled in cuboid A is 16.
  [Count the number of small cubes in cuboid A.]
Step: 3
Volume of A = 16 × 1 m3 = 16 m3
Step: 4
Number of small cubes filled in cuboid B is 24.
  [Count the number of small cubes in cuboid B.]
Step: 5
Volume of B = 24 × 1 m3 = 24 m3
Step: 6
Total volume = Volume of A + Volume of B = 16 m3 + 24 m3 = 40 m3
Step: 7
Volume of the composite 3-D shape is 40 m3.
Correct Answer is :   40 m3
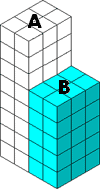
Q12Find the volume of the composite 3-D shape shown, where each small cube measures 1 m3.


A. 72 m3
B. 78 m3
C. 60 m3
D. 69 m3

Solutions
Share 
Step: 1
To find the volume of the composite 3-D shape, count the number of small cubes in both A and B and add.
Step: 2
Number of small cubes filled in cuboid A is 48.
  [Count the number of small cubes in cuboid A.]
Step: 3
Volume of A = 48 × 1 m3 = 48 m3
Step: 4
Number of small cubes filled in cuboid B is 30.
  [Count the number of small cubes in cuboid B.]
Step: 5
Volume of B = 30 × 1 m3 = 30 m3
Step: 6
Total volume = Volume of A + Volume of B = 48 m3 + 30 m3 = 78 m3
Step: 7
Volume of the composite 3-D shape is 78 m3.
Correct Answer is :   78 m3
Q13Find the volume of the composite 3-D shape shown, where each small cube measures 1 m3.

A. 36 m3
B. 30 m3
C. 38 m3
D. 40 m3

Solutions
Share 
Step: 1
To find the volume of the composite 3-D shape, count the number of small cubes in both A and B and add.
Step: 2
Number of small cubes filled in cuboid A is 12.
  [Count the number of small cubes in cuboid A.]
Step: 3
Volume of A = 12 × 1 m3 = 12 m3
Step: 4
Number of small cubes filled in cuboid B is 18.
  [Count the number of small cubes in cuboid B.]
Step: 5
Volume of B = 18 × 1 m3 = 18 m3
Step: 6
Total volume = Volume of A + Volume of B = 12 m3 + 18 m3 = 30 m3
Step: 7
Volume of the composite 3-D shape is 30 m3.
Correct Answer is :   30 m3
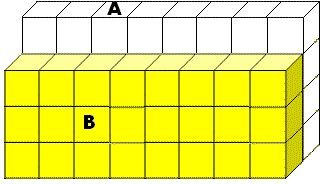
Q14Find the volume of the composite 3-D shape shown if the volume of each small cube is 1 cm3.


A. 56 cm3
B. 32 cm3
C. 24 cm3
D. 54 cm3

Solutions
Share 
Step: 1
To find the volume of the composite 3-D shape, count the number of small cubes in both A and B and add.
Step: 2
Number of small cubes filled in cuboid A is 32.
Step: 3
Volume of A is 32 × 1 cm3 = 32 cm3
Step: 4
Number of small cubes filled in cuboid B is 24.
Step: 5
Volume of B is 24 × cm3 = 24 cm3
Step: 6
Total Volume = Volume of A + Volume of B = 32 cm3 + 24 cm3 = 56 cm3
Step: 7
Volume of the composite 3-D shape is 56 cm3.
Correct Answer is :   56 cm3

HighSchool Math