Solved Examples and Worksheet for Dividing Fraction by a Whole Number and vice versa

Q1Jerald read 15 of a book in 4 hours. What fraction of the book did he read in an hour?
A. 15
B. 120
C. 520
D. 420

Solutions
Share 
Step: 1
15 ÷ 4
  [Write the division sentence.]
Step: 2
= 15 ÷ 41
  [Write the whole number as a fraction.]
Step: 3
= 15 × 14
  [Multiply by the reciprocal of 41, which is 14 .]
Step: 4
= 1×15×4
  [Multiply the numerators and denominators.]
Step: 5
= 120
  
Step: 6
So, Jerald read 120 of the book in an hour.
Correct Answer is :   120
Q2Jessica spent 14 of her money to buy 2 Pokemon toys. What fraction of her money did she spend to buy one Pokemon toy?

A. 8
B. 12
C. 24
D. 18

Solutions
Share 
Step: 1
14 ÷ 2
  [Write the division sentence.]
Step: 2
= 14 ÷ 21
  [Write the whole number as a fraction.]
Step: 3
= 14 × 12
  [Multiply by the reciprocal of 21, which is 12 .]
Step: 4
= 1×14×2
  [Multiply the numerators and denominators.]
Step: 5
= 18
  
Step: 6
So, Jessica spent 18 of her money to buy one Pokemon toy.
Correct Answer is :   18
Q34 similar books occupy 16 of the space in a shelf. What fraction of the shelf does each book occupy?

A. 24
B. 23
C. 14
D. 124

Solutions
Share 
Step: 1
16 ÷ 4
  [Write the division sentence.]
Step: 2
= 16 ÷ 41
  [Write the whole number as a fraction.]
Step: 3
= 16 × 14
  [Multiply by the reciprocal of 41, which is 14 .]
Step: 4
= 1×16×4
  [Multiply the numerators and denominators.]
Step: 5
= 124
  
Step: 6
So, each book occupies 124 of the space in the shelf.
Correct Answer is :   124
Q450 marbles weigh 16 lb. What is the weight of each marble?

A. 813 lb
B. 1300 lb
C. 150 lb
D. 300 lb

Solutions
Share 
Step: 1
16 ÷ 50
  [Write the division sentence.]
Step: 2
= 16 ÷ 501
  [Write the whole number as a fraction.]
Step: 3
= 16 × 150
  [Multiply by the reciprocal of 501, which is 150 .]
Step: 4
= 1×150×6
  [Multiply the numerators and denominators.]
Step: 5
= 1300
  
Step: 6
So, weight of each marble is 1300lb.
Correct Answer is :   1300 lb
Q5Edward is distributing shirts in an orphanage. He distributed 15 of the shirts he brought to 12 kids. What fraction of the total shirts did each child get?
A. 60
B. 160
C. 512
D. 15

Solutions
Share 
Step: 1
15 ÷ 12
  [Write the division sentence.]
Step: 2
= 15 ÷ 121
  [Write the whole number as a fraction.]
Step: 3
= 15 × 112
  [Multiply by the reciprocal of 121, which is 112 .]
Step: 4
= 1×15×12
  [Multiply the numerators and denominators.]
Step: 5
= 160
  
Step: 6
So, each child got 160 of the total number of shirts that Edward brought.
Correct Answer is :   160
Q6Brad and his friends went to an Opera. He spent 14 of his money to buy 17 tickets. What fraction of his money did Brad spend on each ticket?
A. 14
B. 168
C. 68
D. 417

Solutions
Share 
Step: 1
14 ÷ 17
  [Write the division sentence.]
Step: 2
= 14 ÷ 171
  [Write the whole number as a fraction.]
Step: 3
= 14 × 117
  [Multiply by the reciprocal of 171, which is 117 .]
Step: 4
= 1×14×17
  [Multiply the numerators and denominators.]
Step: 5
= 168
  
Step: 6
So, Brad spent 168 of his money on each ticket.
Correct Answer is :   168
Q7How many 12 cup servings are there in a 10 cup pitcher of juice?

A. 18
B. 24
C. 21
D. 20

Solutions
Share 
Step: 1
Number of servings = Total Amount of Juice ÷ Amount of juice in 1 serving.
Step: 2
Number of servings = 10 ÷ 12.
Step: 3
= 101 ÷ 12.
  [Write 10 as 101.]
Step: 4
= 101× 21.
  [Multiply by the reciprocal of 12 which is 21.]
Step: 5
= 10×21×1 = 201.
  [Multiply the numerators and the denominators.]
Step: 6
The number of servings = 20
Correct Answer is :   20
Q8Milkman Ted wants to pour 5 liters of milk into 12 liter bottles. How many 12 liter bottles does he need?

A. 15
B. 52
C. 24
D. 10

Solutions
Share 
Step: 1
Number of 12 liter bottles = total amount of milk ÷ amount of milk in 1 smaller bottle
Step: 2
Number of 12 liter bottles = 5 ÷ 12.
Step: 3
= 51 ÷ 12.
  [Write 5 as 51.]
Step: 4
= 51 × 21.
  [Multiply by the reciprocal of 12 which is 21.]
Step: 5
= 5×21×1 = 101.
  [Multiply the numerators and the denominators.]
Step: 6
Ted needs 10 bottles of 12 liter each to pour 5 liters of milk.
Correct Answer is :   10
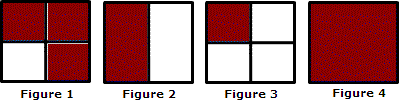
Q9Tom bought 12 liter of coke. He served it to 2 people. Which of the following figures represent the amount of coke that each of them got?

A. Figure 2
B. Figure 4
C. Figure 3
D. Figure 1

Solutions
Share 
Step: 1
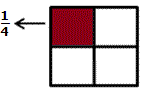
A square represents 1 whole (1 liter of coke).
Step: 2
Divide the square vertically into 2 equal parts. Each part represents 12 liter of Coke.
Step: 3
Again divide the square into 2 horizontal sections.
  [Since the coke is to be shared by 2 persons.]

Step: 4
We get a total of 4 parts. One part out of a total of 4 parts i.e., 14 liters is what each person got. Thus 12 liter is divided into 2 equal parts of 14 liter each.
Correct Answer is :   Figure 3
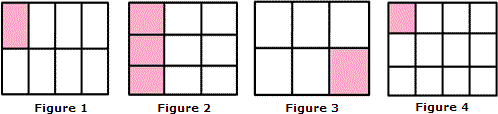
Q10Mr. Neil distributes 14 pound of jellybeans equally among 3 children. Which of the following figures represent the amount of jellybeans that each child gets?


A. Figure 4
B. Figure 2
C. Figure 1
D. Figure 3

Solutions
Share 
Step: 1
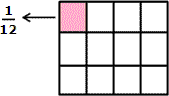
A square represents 1 whole( 1 lb of candy).
Step: 2
Divide the square vertically into 4 equal parts. Each part represents 14 lb of candy.
Step: 3
Again divide the square into 3 horizontal sections.
   [Since the candy is to be shared by 3 persons.]

Step: 4
We get a total of 12 parts. One part out of a total of 12 parts i.e., 112 lb is what each person will get. Thus 14 lb is divided into 3 equal parts of 112 lb each.
Correct Answer is :   Figure 4
Q11Find the value of 35 ÷ 110 .

A. 35
B. 3.5
C. 3500
D. 350

Solutions
Share 
Step: 1
35 ÷ 110
  [Given.]
Step: 2
= 351 × 101
Step: 3
= 3501
Step: 4
= 350
Step: 5
The value of 35 ÷ 110 = 350.
Correct Answer is :   350
Q12Find the value of 56 ÷ 114 .

A. 784
B. 5624
C. 10796
D. 5426

Solutions
Share 
Step: 1
56 ÷ 114
  [Given.]
Step: 2
= 561 × 141
Step: 3
= 7841
Step: 4
= 784
Step: 5
The value of 56 ÷ 114 = 784.
Correct Answer is :   784
Q13Find the value of 35 ÷ 15 .
A. 136
B. 6.8
C. 1235
D. 175

Solutions
Share 
Step: 1
35 ÷ 15
  [Given.]
Step: 2
= 351 × 51
Step: 3
= 1751
Step: 4
= 175
Step: 5
The value of 35 ÷ 15 = 175.
Correct Answer is :   175
Q14Find the value of 17 ÷ 14 .

A. 68
B. 4.25
C. 44
D. 85

Solutions
Share 
Step: 1
17 ÷ 14
  [Given.]
Step: 2
= 171 × 41
Step: 3
= 681
Step: 4
= 68
Step: 5
The value of 17 ÷ 14 = 68.
Correct Answer is :   68
Q15Find the value of 21 ÷ 17 .

A. 161
B. 3
C. 147
D. 154

Solutions
Share 
Step: 1
21 ÷ 17
  [Given.]
Step: 2
= 211 × 71
Step: 3
= 1471
Step: 4
= 147
Step: 5
The value of 21 ÷ 17 = 147.
Correct Answer is :   147

HighSchool Math