Definition Of Triangle Proportionality Theorem

Triangle Proportionality Theorem states that a line drawn parallel to any of the sides of a triangle divides the other two sides proportionally.

Example of Triangle Proportionality Theorem

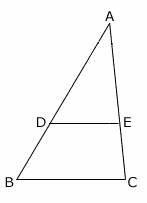
In the given triangle ABC, BC is the base of the triangle.
DE is drawn parallel to BC and it intersects the other two sides AB and AC at D and E respectively. 
Here,  = .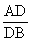
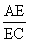This is called triangle proportionality theorem.

Video Examples: Key Stage 1 Maths: Addition

Solved Example on Triangle Proportionality Theorem

Ques: QP || BC. If AQ = 3 cm, PC = 4 cm, QB = 11 cm, and BC = 12 cm, then find the length of AP rounded to the nearest decimal.

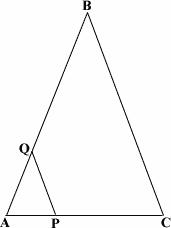
Choices:

A. 2.59 cm
B. 1.09 cm
C. 2.09 cm
D. 1.59 cm
Correct Answer: B

Solution:

Step 1: A line drawn parallel to any of the sides of a triangle divides the other two sides proportionally.
Step 2: 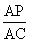 =  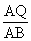[Proportionality Theorem.]
Step 3:  [Substitute the values.]
Step 4: 14(AP) = 3(AP) + 12 [Cross multiplication.]
Step 5: 11(AP) = 12 [Simplify.]
Step 6: AP = 1.09 [Divide by 11 on both sides.]
Step 7: The length of AP is 1.09 cm.

Related Worksheet

• Finding-Missing-Angles-in-Polygons-Gr-7