Finding Missing Angles in Polygons-Gr 7-Solved Examples

Solved Examples and Worksheet for Finding Missing Angles in Polygons

Q1Find the measure of ∠A, if ∠C = 61° and ∠B = 60°.

A. 47°
B. 59°
C. 71°
D. 44°

Solutions

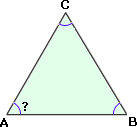
Step: 1

The sum of three angles in a triangle is 180°.

Step: 2

∠ A + ∠ B + ∠ C = 180°.

Step: 3

∠ A + 60° + 61° = 180°

[Substitute ∠ B = 60° and ∠ C = 61°.]

Step: 4

∠ A + 121° = 180°

[Combine like terms.]

Step: 5

∠ A = 180° - 121°

[Subtract 121° from both sides.]

Step: 6

∠ A = 59°

Correct Answer is : 59°

Q2Find ∠A and ∠B for the triangle ABC, if ∠C = 34°.

A. 93°
B. 107°
C. 83°
D. 73°

Solutions

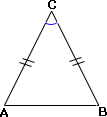
Step: 1

From the figure, AC = BC.

Step: 2

So, ΔABC is isosceles and ∠A = ∠B.

Step: 3

Let ∠A = ∠B = x

Step: 4

In a triangle, the sum of all the angles is equal to 180°.

Step: 5

∠A + ∠B + ∠C =180°

Step: 6

x + x + 34° = 180°

[Substitute ∠A = ∠B = x and ∠C = 34°.]

Step: 7

2x = 180° - 34°

[Subtract 34° from each side.]

Step: 8

2x = 146°

Step: 9

x = 146°2

[Divide each side by 2.]

Step: 10

x = 73°

Correct Answer is : 73°

Q3ΔABC is an isosceles triangle and ∠A = 30°. Which of the following cannot be the measures of other two angles?

A. 40°, 120°
B. 75°, 75°
C. 30°, 120°
D. None of the above

Solutions

Step: 1

In an isosceles triangle, two angles are equal.

Step: 2

A triangle with angle measures 30°, 30°, 120° and 30°, 75°, 75° forms an isosceles triangle.

Step: 3

Among the choices, a triangle with angle measures 30°, 40°, and 120° cannot form an isosceles triangle.

Correct Answer is : 40°, 120°

Q4Three angles of a quadrilateral are 123^o, 57^o, and 97^o. What is the measure of the fourth angle?
A. 69.25^o
B. 83^o
C. 277^o
D. 123^o

Solutions

Step: 1

Sum of the four angle measures in a quadrilateral is 360^o.

Step: 2

Let x be the measure of the fourth angle.

Step: 3

x + 123^o + 57^o + 97^o = 360^o

Step: 4

x + 277^o = 360^o

Step: 5

x = 360^o - 277^o

[Subtract 277 from both sides.]

Step: 6

x = 83^o

Step: 7

So, the measure of the fourth angle is 83^o.

Correct Answer is : 83^o

Q5m∠A = 50° in the parallelogram ABCD. Find the measures of ∠B, ∠C and ∠D.

A. 50°, 50°, 50°
B. 130°, 50°, 50°
C. 130°, 50°, 130°
D. None of the above

Solutions

Step: 1

The adjacent angles in a parallelogram are supplementary.

Step: 2

In parallelogram ABCD, ∠A and ∠B are adjacent angles.

Step: 3

m∠A + m∠B = 180°

Step: 4

50° + m∠B = 180°

[Substitute m∠A = 50°.]

Step: 5

∠B = 180° - 50°

[Subtract 50° on both sides.]

Step: 6

m∠B = 130°

Step: 7

In a parallelogram, opposite angles are congruent.

Step: 8

∠A and ∠C are opposite angles.

Step: 9

m∠C = m∠A = 50°

Step: 10

∠B and ∠D are opposite angles.

Step: 11

m∠D = m∠B = 130°

Step: 12

m∠B = 130°, m∠C = 50° and m∠D = 130°

Correct Answer is : 130°, 50°, 130°

Q6The sum of two angles in a triangle is 120°. Find the third angle.

A. 40°
B. 65°
C. 60°
D. 240°

Solutions

Step: 1

The sum of three angles in a triangle is 180°.

Step: 2

Let x be the third angle.

Step: 3

x + Sum of the other two angles = 180°

Step: 4

x + 120° = 180°

[Substitute sum of two angles = 120°.]

Step: 5

x = 180° - 120°

[Subtract 120° from each side.]

Step: 6

x = 60°

Step: 7

The third angle is 60°.

Correct Answer is : 60°

Q7If two angles of a triangle measure 50 and 40, then find the measure of the third angle.

A. 85
B. 90
C. 95
D. 80

Solutions

Step: 1

The sum of the measures of all the three angles of a triangle is 180.

Step: 2

The measure of the third angle = 180 - (50 + 40).

Step: 3

= 90

[Simplify]

Step: 4

So, the measure of the third angle is 90.

Correct Answer is : 90

Q8Find the measure of x in the quadrilateral.

A. 121°
B. 110°
C. 109°
D. 100°

Solutions

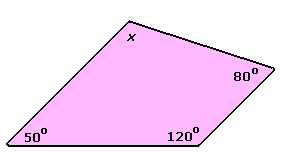
Step: 1

The given diagram is a quadrilateral with four angles.

Step: 2

In a quadrilateral, the sum of the four angles = 360°

Step: 3

So, ∠50 + ∠120 + ∠ 80 + ∠x = 360°

Step: 4

∠250 + ∠x = 360°

Step: 5

Therefore, ∠x = 360° - 250° = 110°

Correct Answer is : 110°

Q9Find the measure of the unknown angle.

A. 75°
B. 100°
C. 85°
D. 101°

Solutions

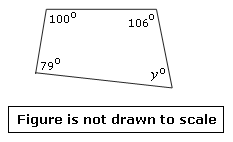
Step: 1

The given diagram is a quadrilateral with four angles.

Step: 2

In a quadrilateral, the sum of the four angles = 360°.

Step: 3

So, 79° + 100° + 106° + y° = 360°.

Step: 4

y° + 285° = 360°

Step: 5

Therefore, y° = 360° - 285° = 75°.

[Simplify.]

Correct Answer is : 75°

Q10In quadrilateral PQRS, m∠P = 87°, m∠Q = 78°, and m∠R = 90°. Find the m∠S.

A. 100°
B. 105°
C. 45°
D. 205°

Solutions

Step: 1

In a quadrilateral, the sum of the four angles = 360°.

Step: 2

m∠P + m∠Q + m∠R + m∠S = 360°

[PQRS is a quadrilateral.]

Step: 3

87° + 78° +90° + m∠S = 360°

[Substitute the given values.]

Step: 4

255° + m∠S = 360°

[Simplify.]

Step: 5

m∠S = 360° - 255° = 105°

[Subtract.]

Step: 6

So, m∠S is 105°.

Correct Answer is : 105°

Q11Find the measure of the unknown angle.

A. 125°
B. 128°
C. 50°
D. 232°

Solutions

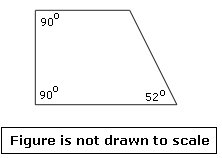
Step: 1

Let the unknown angle be x.

Step: 2

90° + 90° + 52° + x° = 360°

[The given figure is a quadrilateral.]

Step: 3

232° + x° = 360°

[Simplify.]

Step: 4

x° = 360° - 232° = 128°

[Subtract.]

Step: 5

So, the measure of the unknown angle is 128°.

Correct Answer is : 128°

Q12Three angles of a quadrilateral are 82°, 65°, 93°. What is the measure of the fourth angle?

A. 120°
B. 110°
C. 150°
D. 80°

Solutions

Step: 1

Sum of the four angle measures in a quadrilateral is 360°.

Step: 2

Let x be the measure of the fourth angle.

Step: 3

x + 82° + 65° + 93° = 360°

Step: 4

x + 240° = 360°

Step: 5

x = 360° - 240°

[Subtract 240 from both sides.]

Step: 6

x = 120°

Step: 7

So, the measure of the fourth angle is 120°.

Correct Answer is : 120°

Q13Three angles of a quadrilateral are 120°, 55°, and 75°. What is the measure of the fourth angle?
A. 95°
B. 100°
C. 110°
D. 105°

Solutions

Step: 1

Sum of the four angle measures in a quadrilateral is 360°.

Step: 2

Let x be the measure of the fourth angle.

Step: 3

x + 120° + 55° + 75° = 360°.

Step: 4

x = 360° - 250°

[Subtract 250 from both sides.]

Step: 5

x = 110°

Step: 6

So, the measure of the fourth angle is 110°.

Correct Answer is : 110°

Q14If x = 62°, then find the missing angle shown in the figure.

A. 28°
B. 45°
C. 36°
D. cannot be determined

Solutions

Step: 1

The sum of all the angle measures of a triangle is 180°.

Step: 2

90° + 62° + y° = 180°

[Equate the sum of angles of the triangle to 180°.]

Step: 3

152° + y° = 180°

[Add.]

Step: 4

y° = 28°

[Subtract 152° from each side.]

Correct Answer is : 28°

Q15Find the measure of the third angle.

A. 120°
B. 100°
C. 90°
D. 110°

Solutions

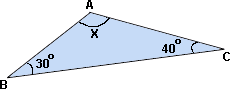
Step: 1

The sum of all the angle measures of a triangle is 180°.

Step: 2

In the triangle, the sum of all the 3 angles measures is 30° + 40° + X.

Step: 3

30° + 40° + X = 180°

[Equate the sum of all the three angles measures of the triangle to 180°.]

Step: 4

70° + X = 180°

Step: 5

X = 110°

[Subtract 70° on both sides.]

Step: 6

So, the measure of the third angle of the triangle is 110°.

Correct Answer is : 110°

Solved Examples and Worksheet for Finding Missing Angles in Polygons

Related Worksheet

Related Topic

HighSchool Math