Quadratic Equation
Definition Of Quadratic Equation
A Quadratic Equation is one that can be written in the standard form ax2 + bx + c = 0, where a, b, and c are real numbers and a does not equal zero.
More About Quadratic Equation
In any quadratic equation, the highest power of an unknown quantity is 2.
A quadratic equation can contain one or more second power variables.
A quadratic equation has at most two solutions.
The graph of a quadratic equation is a parabola.
Video Examples: Introduction to the quadratic equation
Example of Quadratic Equation
7x2 + 9x + 2 = 0 is a quadratic equation, because this equation is in the form ax2 + bx + c = 0, where a = 7, b = 9, and c = 2 and the variable is a second degree variable.
Solved Example on Quadratic Equation
Ques: Which of the following is a quadratic equation?
Choices:
A. x2 + 5x + 1 = 0
B. (3x - 1) (2x + 1) (x + 3) = 0
C. x + 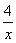 = x2
= x2
D. x (x2 - 1) - 4x + 28 = 0
Correct Answer: A
Solution:
Step 1: A quadratic equation can be expressed in the form ax2 + bx + c = 0.
Step 2: Here, the only equation that has a second degree variable is x2 + 5x + 1 = 0 and all other equations have third degree variables.
Step 3: So, the quadratic equation is x2 + 5x + 1 = 0.