Law Of Cosines
Definition Of Law Of Cosines
Law of Cosines is an equation relating the lengths of the sides of a cosine of one of its angles.
More About Law of Cosines
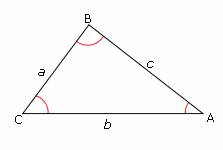
For any triangle ABC, where a, b, and c are the lengths of the sides opposite to the angles A, B, and C respectively, the Law of cosines states that:
a2 = b2+ c2- 2bc cos A
b2 = a2 + c2 - 2ac cos B
c2 = a2 + b2 - 2ab cos C
Law of cosines is also called as cosine rule or cosine formula.
Video Examples: Law of Cosines
Example of Law of Cosines
The figure below shows two of the six Law of Cosiness of a cube In triangle ABC, if a = 19, b = 12, and c = 10 are the lengths of the sides opposite to the angles A, B, and C respectively, then, by using law of cosines, the measure of angle A can be obtained this way:
a2 = b2+ c2- 2bc cos A
Cos A = b2+ c2 - a2/ 2bc
Cos A = 122 + 102 - 192/ 2(12) (10)
Cos A = - 0.4875
∠ A = 119°
Solved Example on Law of Cosines
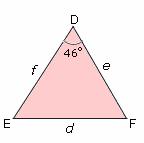
Ques: In â–³DEF, if angle D = 46°, f = 10, and e = 17, then find the length of d to two significant digits
Choices:
A. 27
B. 20
C. 12
D. 25
Correct Answer: C
Solution:
Step 1: d2 = 172 + 102 - 2 (17) (10) cos 46° [Use law of cosines: d2 = e2+ f2- 2ef cos D.]
Step 2: d2 ~ 152.816154
Step 3: d = 12, to two significant digits. [Simplify.]