COPLANAR
Definition Of Coplanar
A set of points, lines, line segments, rays or any other geometrical shapes that lie on the same plane are said to be Coplanar.
More About Coplanar
Parallel lines in three-dimensional space are coplanar, but skew lines are not.
Example of Coplanar
All the points A, B, C, and D in the plane P are coplanar
Video Examples: What are coplanar points
Solved Example on Coplanar
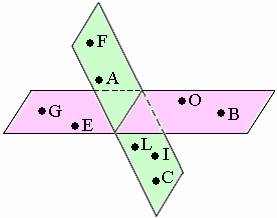
Choose the Correct Statement/Statements.
1. Points F, A, L, I, C, G, E, O, and B are coplanar.
2. Points G, E, F, and A are coplanar.
3. O, A, and B are coplanar.
4. Points F, A, L, I, C are coplanar.
Choices:
A. 1 and 2 only
B. 3 and 4 only
C. 4 only
D. 1 only
Correct Answer: C
Solution:
Step 1: A plane is a flat surface that extends in all directions.
Step 2: F, A, L, I, C lie on plane F and G, E, O, B lie on plane G. So, the first statement is false. [A plane can be named either by a single capital letter or by naming at least three non-collinear points in the plane.]
Step 3: Points G, E and F, A lie on two different planes. So, they are not coplanar. So, second statement is false.
Step 4: O and A lie on two different planes. So, they are not coplanar. Therefore, the third statement is also false.
Step 5: Points F, A, L, I, C lie on the same plane and are coplanar. So, the fourth statement is correct.
Quick Summary
- Coplanar objects exist within the same plane.
- Parallel lines in 3D space are coplanar.
- Skew lines are not coplanar.
🍎 Teacher Insights
Use physical models (e.g., cardboard planes and straws as lines) to illustrate coplanar and non-coplanar relationships. Emphasize the difference between coplanar and collinear.🎓 Prerequisites
- Points
- Lines
- Planes
- Basic Geometric Definitions
Check Your Knowledge
Q1: Which of the following statements is true about coplanar points?
Q2: If four points do not lie in the same plane, then they are...
Frequently Asked Questions
Q: Are two intersecting lines always coplanar?
A: Yes, two intersecting lines define a plane and are therefore coplanar.
Q: Are two parallel lines always coplanar?
A: Yes, two parallel lines define a plane and are therefore coplanar.