Related Links
Centroid
Definition Of Centroid
Centroid of a triangle is the point of intersection of all its three medians.
The centre of mass of a uniform object is also called as Centroid.
More About Centroid
The centroid of a triangle divides the medians in the ratio 2:1.
Video Examples: Centroid
Example of Centroid
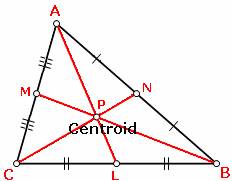
In the above triangle, AL, BM, CN are the medians of the triangle and they intersect at the point P. So, the point P is the centroid of the triangle.
Solved Example onCentroid
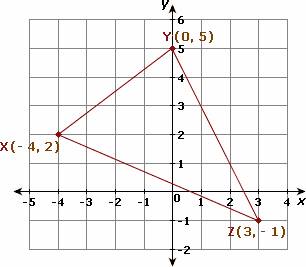
Ques: Find the coordinates of the centroid of â–³XYZ with X (- 4, 2), Y (0, 5), and Z (3, - 1).
Choices:
A. (- 1/3, 2)
B. (1/3, 2)
C. (- 1/3, - 2)
D. (- 1/3, - 1/2)
Correct Answer: A
Solution:
Step 1: The centroid of a triangle is the mean of the X-coordinates and the mean of the Y-coordinates of the triangle's vertices.
Step 2: The mean of the X-coordinates is (- 4 + 0 + 3)/3 = - 1/3.
Step 3: The mean of the Y-coordinates is (2 + 5 + (- 1))/3 = 2.
Step 4: The coordinates of the centroid is (- 1/3, 2).