Solved Examples and Worksheet for ASA and AAS Postulates -Triangle Congruence

Q1Which of the following can be used to prove that ΔABE ≅ ΔCBD from the figure ?

A. SAS
B. ASA
C. RHS
D. AAA

Solutions
Share 
Q2Which of the following is true?


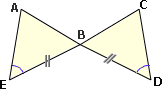
A. ΔACB ≅ ΔCDA
B. ΔABC ≅ ΔADC
C. ΔABC ≅ ΔDAC
D. ΔACB ≅ ΔCAD

Solutions
Share 
Step: 1
If two angles and the included side of one triangle are congruent to the two angles and the included side of another triangle, then the two triangles are congruent.
Step: 2
As ∠CAB ≅ ∠ACD, AC¯ = AC¯ and ∠ACB ≅ ∠CAD, by ASA Postulate, we have ΔACB ≅ ΔCAD.
Correct Answer is :   ΔACB ≅ ΔCAD
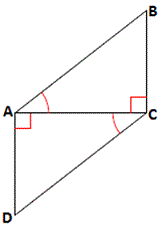
Q3Which of the following can be applied directly to prove that ΔABC ≅ Δ EDC ?


A. AAS postulate
B. ASA postulate
C. SAS postulate
D. SSS postulate

Solutions
Share 
Step: 1
AB¯ = DE¯
  [Given.]
Step: 2
∠BAC = ∠DEC
  [Given.]
Step: 3
∠ACB = ∠ECD
  [Vertical angles are congruent.]
Step: 4

Step: 5
If the two angles and the non included side of one triangle are congruent to the two angles and the non included side of another triangle, then the two triangles are congruent.
  [AAS postulate.]
Step: 6
Therefore, ΔABC ≅ Δ EDC by AAS postulate.
Correct Answer is :   AAS postulate
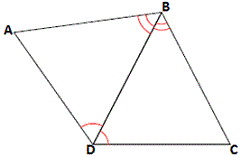
Q4Which of the following can be applied directly to prove that ΔABD ≅ ΔCBD ?

A. SAS postulate
B. SSS postulate
C. ASA postulate
D. AAS postulate

Solutions
Share 
Step: 1
∠ADB = ∠CDB
  [Given.]
Step: 2
∠ABD = ∠CBD
  [Given.]
Step: 3
BD¯ = BD¯
  [Reflexive property of congruence.]
Step: 4
If two angles and included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent.
  [ASA postulate.]
Step: 5
Therefore, ΔABD ≅ ΔCBD by ASA postulate.
Correct Answer is :   ASA postulate
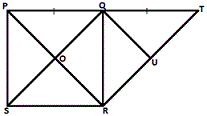
Q5PQRS is a square, and U is the midpoint of line segment RT. Find the number of triangles that are congruent to ΔUQT with respect to ASA Theorem.


A. 3
B. 5
C. 6
D. 4

Solutions
Share 
Step: 1
PQ¯ = QR¯ = RS¯ = SP¯
  [PQRS is s square.]
Step: 2
PQ¯ = QT¯
  [Given.]
Step: 3
⇒ PQ¯ = QR¯ = RS¯ = SP¯ = QT¯
  [From Step 1.]
Step: 4
All four angles of a square are equal to 90°. The diagonals of the square bisect its angles.
Step: 5
⇒ ∠OQP = ∠OPQ = ∠OQR = ∠ORQ = ∠ORS = ∠OSR = ∠OSP = ∠OPS = 45°
Step: 6
∠QRT = ∠QTR = 45°
  [∠RQT = 90° and QR¯ = QT¯.]
Step: 7
UQ¯ bisects ∠RQT. So, ∠UQR = ∠UQT = 45°
  [U is the midpoint of line segment RT.]
Step: 8
If two angles and included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent.
Step: 9
Therefore, ΔOPQ ≅ ΔOQR ≅ ΔORS ≅ ΔOSP ≅ ΔURQ ≅ ΔUQT.
Correct Answer is :   6
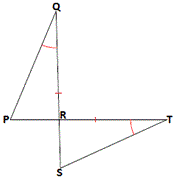
Q6Which of the following can be applied directly to prove that ΔPQR ≅ ΔSTR ?

A. ASA postulate
B. AAS postulate
C. SAS postulate
D. SSS postulate

Solutions
Share 
Step: 1
∠PQR = ∠STR
  [Given.]
Step: 2
∠PRQ = ∠SRT
  [Vertical angles are congruent.]
Step: 3
QR¯ = TR¯
  [Given.]
Step: 4
If two angles and included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent.
Step: 5
Therefore, ΔPQR ≅ ΔSTR by ASA postulate.
Correct Answer is :   ASA postulate
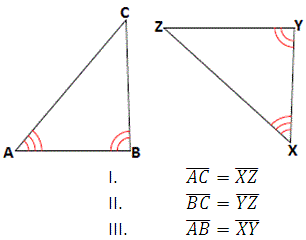
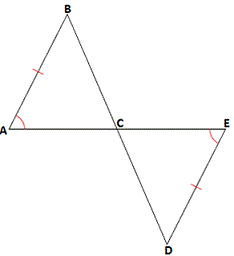
Q7What additional information is needed to prove that ΔABC ≅ ΔXYZ by the AAS Theorem.

A. I only
B. II only
C. Either I or II
D. III only

Solutions
Share 
Step: 1
∠CAB = ∠ZXY
  [Given.]
Step: 2
∠ABC = ∠XYZ
  [Given.]
Step: 3
If the two angles and the non included side of one triangle are congruent to the two angles and the non included side of another triangle, then the two triangles are congruent.
  [AAS Theorem.]
Step: 4
The non included sides of ΔABC are AC, BC and that of ΔXYZ are XZ, YZ.
Step: 5
Therefore, ΔABC ≅ ΔXYZ if either AC¯ = XZ¯ or BC¯ = YZ¯.
Step: 6
But, only the information BC¯ = YZ¯ will be need to prove that ΔABC = ΔXYZ by the AAS theorem.
Correct Answer is :    II only
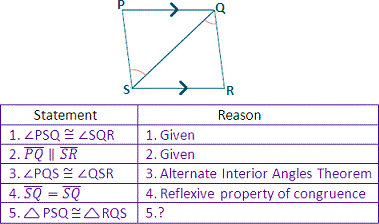
Q8Supply the reason to complete the proof below:


A. ASA postulate
B. AAS postulate
C. SAS postulate
D. SSS postulate

Solutions
Share 
Step: 1
If two angles and included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent.
  [ASA postulate.]
Step: 2
As ∠PSQ ≅ ∠RQS, ∠PQS ≅ ∠RSQ and SQ¯ = SQ¯, by ASA postulate, we have ΔPSQ ≅ΔRQS.
Correct Answer is :   ASA postulate
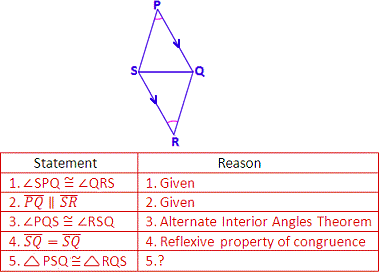
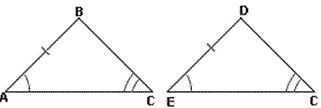
Q9Supply the reason to complete the proof below:

A. SSS postulate
B. ASA postulate
C. AAS postulate
D. SAS postulate

Solutions
Share 
Step: 1
If two angles and a non included side of one triangle are congruent to the two angles and the non included side of another triangle, then the two triangles are congruent.
Step: 2
As ∠SPQ ≅ ∠QRS, ∠PQS ≅ ∠QSR and SQ¯ = SQ¯, by AAS postulate, we have ΔPQS ≅ ΔRSQ.
Correct Answer is :   AAS postulate
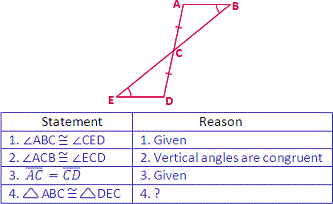
Q10Supply the reason to complete the proof below:

A. ASA postulate
B. AAS postulate
C. SAS postulate
D. SSS postulate

Solutions
Share 
Step: 1
If two angles and a non included side of one triangle are congruent to the two angles and the non included side of another triangle, then the two triangles are congruent.
Step: 2
As ∠ABC ≅ ∠CED, ∠ACB ≅ ∠ECD and AC¯ = CD¯, by AAS theorem, we have ΔABC ≅ ΔDEC
Correct Answer is :   AAS postulate
Q11Supply the reason to complete the proof below:
Given : AB¯ ≅ DE¯

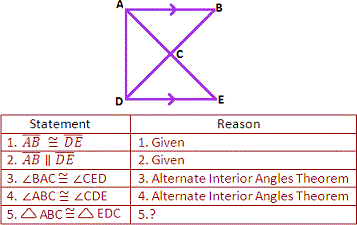
A. AAS postulate
B. SAS postulate
C. SSS postulate
D. ASA postulate

Solutions
Share 
Step: 1
If two angles and included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent.
  [ASA Theorem.]
Step: 2
As ∠BAC ≅ ∠CED, ∠ABC ≅ ∠CDE and AB¯ ≅ DE¯, by ASA theorem, we have ΔABC ≅ ΔEDC
Correct Answer is :   ASA postulate
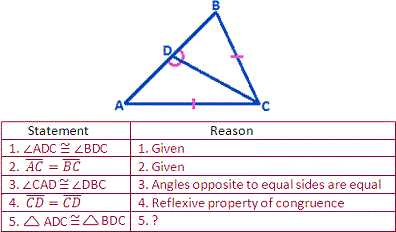
Q12Supply the reason to complete the proof below:


A. SAS postulate
B. AAS postulate
C. SSS postulate
D. ASA postulate

Solutions
Share 
Step: 1
If two angles and a non included side of one triangle are congruent to the two angles and the non included side of another triangle, then the two triangles are congruent.
  [AAS Theorem.]
Step: 2
As ∠ADC ≅ ∠BDC, ∠CAD ≅ ∠DBC and CD¯ = CD¯, by AAS theorem, we have ΔADC ≅ ΔBDC.
  [AAS Theorem.]
Correct Answer is :   AAS postulate

HighSchool Math