SAA CONGRUENCY POSTULATE

SAA Congruency Postulate

Definition Of SAA Congruency Postulate

If two angles and the included side of one triangle are congruent to the two angles and the included side of another triangle, then the two triangles are congruent.

Video Examples: SAA Congruency Postulate

Example of SAA Congruency Postulate

The triangles ABC and PQR are congruent, i.e., ΔABC ≅ ΔPQR, since ∠CAB = ∠RPQ, AC = PR, and ∠ABC = ∠PQR.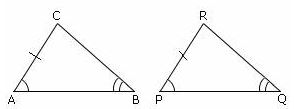

Solved Example on SAA Congruency Postulate

Ques: If the two triangles given are congruent by SAA postulate then identify the value of angle Q.

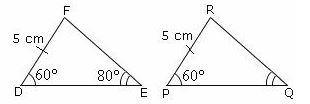
example of SAA Congruency Postulate

Choices:

A. 80°
B. 60°
C. 75°
D. 70°
Correct Answer: A

Solution:

Step 1: If two angles and the non-included side of one triangle is congruent to
two angles and the non-included side of another triangle then the two triangles are congruent by SAA postulate.
Step 2: As the given triangles are congruent by SAA postulate
∠FDE = ∠RPQ, DF= PR, and ∠DEF = ∠PQR.
Step 3: And given ∠DEF = 80° it implies ∠PQR = 80° by SAA postulate.

Quick Summary

SAA postulate is a condition for triangle congruence.
It states that if two angles and the non-included side of one triangle are equal to the corresponding two angles and the non-included side of another triangle, the triangles are congruent.
SAA is equivalent to AAS (Angle-Angle-Side).

\[ null \]

⚠️ Common Mistakes

Confusing SAA with ASA (Angle-Side-Angle) where the side MUST be included between the two angles.
Assuming congruence based on only two angles without considering the side.
Incorrectly identifying corresponding angles and sides.

🌍 Real-World Uses

Construction: Ensuring two triangular roof supports have identical angles and a corresponding non-included side to guarantee they are structurally the same.
Surveying: Using angle measurements and a known side length to determine if two plots of land have the same triangular shape for property division.
Engineering: Verifying that two triangular components of a bridge are congruent based on angle and side measurements to ensure equal stress distribution.

📋 Standards Alignment

CCSS.MATH.CONTENT.HSG.CO.B.7

🔗 Related Links

ASA Congruence Postulate
SAS Congruence Postulate
CPCTC (Corresponding Parts of Congruent Triangles are Congruent)

🍎 Teacher Insights

Use visual aids and hands-on activities to demonstrate the SAA postulate. Emphasize the difference between included and non-included sides. Provide ample practice problems where students have to identify congruent triangles using SAA.

🎓 Prerequisites

Understanding of angles and sides of a triangle
Definition of congruent angles and sides
Basic triangle properties

Check Your Knowledge

Q1: If triangle ABC has angle A = 60 degrees, angle B = 80 degrees, and side BC = 5 cm, and triangle PQR has angle P = 60 degrees, angle Q = 80 degrees, and side QR = 5 cm, are the triangles congruent by SAA?

Yes No Cannot be determined Only if the included side is equal

Q2: Which of the following conditions is sufficient to prove triangle congruence using SAA postulate?

Two angles and the included side of one triangle are congruent to the corresponding parts of another triangle. Two sides and the included angle of one triangle are congruent to the corresponding parts of another triangle. Two angles and a non-included side of one triangle are congruent to the corresponding parts of another triangle. All three sides of one triangle are congruent to the corresponding sides of another triangle.

Frequently Asked Questions

Q: What is the difference between SAA and ASA congruence postulates?
A: In ASA, the side is included between the two angles, whereas in SAA, the side is NOT included between the two angles.

Q: Is SAA the same as AAS?
A: Yes, SAA (Side-Angle-Angle) is the same as AAS (Angle-Angle-Side). The order in which the angles and side are listed does not matter as long as the side is non-included.