REMAINDER
Definition Of Remainder
Remainder is the amount left over after division when one divisor does not divide the dividend exactly.
More about Remainder
Dividend = (Divisor × Quotient) + Remainder
Example of Remainder
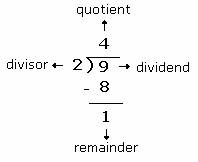
In the above example, 2 is the divisor, 9 is the dividend, 4 is the quotient, and the left over, i.e. 1, is the remainder.
Video Examples: The Remainder Theorem
Solved Example on Remainder
Ques: Divide and write the answer with a remainder 76 ÷ 9.
Choices:
A. 7 r 4
B. 8 r 4
C. 4 r 8
D. 8 r 2
Correct Answer: B
Solution:
Step 1: [Divide.]
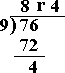
Step 2: So, the answer with remainder is 8 r 4.
Quick Summary
- Remainder is what's left over after dividing.
- Dividend is the number being divided.
- Divisor is the number dividing the dividend.
- Quotient is the result of the division.
⚠️ Common Mistakes
- Forgetting to include the remainder in the final answer.
- Incorrectly calculating the quotient.
🌍 Real-World Uses
- Dividing a pizza: If you have 13 slices of pizza to share equally among 5 friends, each friend gets 2 slices (the quotient), and there are 3 slices left over (the remainder).
- Scheduling tasks: If you need to schedule 23 tasks over 4 days, you can do 5 tasks each day (the quotient), and you'll have 3 tasks left to do on the last day (the remainder).
- Calculating change: If you buy an item for $7 and pay with a $20 bill, you receive $13 in change. If the cashier has only $1 bills and needs to give you the change, 0 twenty dollar bills, 0 ten dollar bills, 1 three dollar bill (made of a two and a one), and 0 in smaller denominations. If change denominations available are only 5,1, a five dollar bill, then eight one dollar bills.
📋 Standards Alignment
CCSS.MATH.CONTENT.4.NBT.B.6CCSS.MATH.CONTENT.5.NBT.B.6
🔗 Related Links
🍎 Teacher Insights
Use real-world examples like sharing cookies or grouping students to illustrate the concept of remainders. Encourage students to check their answers by multiplying the quotient by the divisor and adding the remainder; it should equal the dividend.🎓 Prerequisites
- Division
- Multiplication
Check Your Knowledge
Q1: What is the remainder when 23 is divided by 5?
Q2: If Dividend = 30, Divisor = 7, and Quotient = 4, what is the Remainder?
Frequently Asked Questions
Q: What happens if the remainder is zero?
A: If the remainder is zero, it means the divisor divides the dividend exactly.
Q: Can the remainder be larger than the divisor?
A: No, the remainder must always be smaller than the divisor. If it is larger, it means you can divide further.