INDIRECT MEASUREMENT
Definition Of Indirect Measurement
Indirect measurement is a technique that uses proportions to find a measurement when direct measurement is not possible.
Video Examples: Indirect Measurement
Example of Indirect Measurement
The length of a pole in a picture is given as 4 inches. The scale of the picture is given to be 1 inch : 13 inches. By setting up a proportion, the length n of the actual pole can be found.
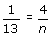
Solving the proportion, we get n = 52 inches.
Solved Example on Indirect Measurement
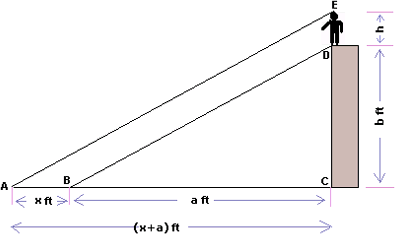
Ques: A boy stands on the top of a building and the total length of shadows of the building and the boy is (x + a) ft and the length of the shadow of the boy alone is x ft. If the height of the building is b ft, then find the height of the boy. [Given x = 8, a = 160, b = 80.]
Choices:
A. 4 ft
B. 3.5 ft
C. 3 ft
D. None of the above
Correct Answer: A
Solution:
Step 1: Let h be the height of the boy.
Step 2: ΔACE ~ ΔBCD, because the measure of angle EAC = measure of angle DBC and the measure of angle C = measure of angle C.
Step 3: Corresponding sides of similar triangles are proportional.
Step 4: The proportion here is:
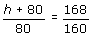Step 5: 160(h + 80) = 168 × 80 [Write the cross products.]
Step 6: 160h + 12,800 = 13,440 [Multiply.]
Step 7: 160h = 640 [Simplify.]
Step 8: h = 4 [Divide both sides by 160 and Simplify.]
Step 9: So, the height of the boy is 4 ft.
Quick Summary
- Indirect measurement uses proportions to find unknown lengths.
- It often involves setting up ratios between corresponding sides of similar figures.
- Scale drawings and shadows are common applications of indirect measurement.
⚠️ Common Mistakes
- Incorrectly setting up the proportion (e.g., not matching corresponding sides).
- Using the wrong units in the proportion.
- Algebra errors when solving for the unknown.
📋 Standards Alignment
CCSS.MATH.CONTENT.7.G.A.1CCSS.MATH.CONTENT.8.G.A.4CCSS.MATH.CONTENT.HSG.SRT.B.5
🍎 Teacher Insights
Use real-world examples to illustrate the concept. Have students measure shadows of objects to determine their heights. Emphasize the importance of accurate measurements and careful setup of the proportion.🎓 Prerequisites
- Ratios
- Proportions
- Similar Triangles
Check Your Knowledge
Q1: A tree casts a shadow of 15 feet. A nearby 5-foot pole casts a shadow of 3 feet. How tall is the tree?
Q2: In a scale drawing, a building is 10 inches tall. The scale is 1 inch : 5 feet. How tall is the actual building?
Frequently Asked Questions
Q: When would you use indirect measurement?
A: When it's impossible or impractical to measure something directly, like the height of a tall building or the distance across a wide river.
Q: How do you know if two triangles are similar?
A: If two angles of one triangle are congruent to two angles of another triangle (AA similarity), or if all three sides are proportional (SSS similarity), or if two sides are proportional and the included angle is congruent (SAS similarity).