DOMAIN
Definition Of Domain
Domain of a relation is the set of all x-coordinates of the ordered pairs of that relation.
Examples of Domain
Domain of the relation {(3,4), (9,8), (4,5)} is {3, 4, 9}.
Video Examples: How to Figure the Domain & Range of Ordered Pairs : Math Tips
Solved Example on Domain
Ques: Find the domain of f(x) = (x + 3)-1.
Choices:
A. (- ∞, - 3) or (- 3, - ∞)
B. (- 3, 3)
C. (- ∞, - 3) or (3, ∞)
D. (- ∞, ∞)
Correct Answer: A
Solution:
Step 1:f(x) = (x + 3)-1.
Step 2: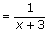 
Step 3: Domain of a function is the set of all possible input values for the function.
Step 4: Observe that the function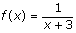 
is not defined only when x = - 3.
Step 5: So, the domain for this function is (- ∞, - 3) or (- 3, - ∞).
Quick Summary
- Domain is the set of all first elements (x-coordinates) in the ordered pairs of a relation.
- The domain represents the set of input values for a function.
⚠️ Common Mistakes
- Confusing domain with range (y-coordinates).
- Forgetting to exclude values that make a function undefined (e.g., division by zero).
🌍 Real-World Uses
- Determining the allowable inputs for a GPS navigation system to calculate a route (e.g., valid starting and ending coordinates).
- Calculating the safe operating range of a machine in a factory by setting input parameters based on physical constraints.
- Analyzing the possible number of items that can be purchased within a specific budget, with the price of each item defining the domain.
📋 Standards Alignment
CCSS.MATH.CONTENT.HSF.IF.A.1
🔗 Related Links
🍎 Teacher Insights
Emphasize the connection between the domain as input values and the x-coordinates of points on a graph. Use visual representations like mapping diagrams to illustrate the concept.🎓 Prerequisites
- Set Theory
- Ordered Pairs
- Functions
Check Your Knowledge
Q1: What is the domain of the relation {(1, 2), (3, 4), (5, 6)}?
Q2: What is the domain of f(x) = 1/(x+3)?
Frequently Asked Questions
Q: What happens if a value in the domain repeats?
A: The domain only includes unique values, so repeated x-coordinates are listed only once.
Q: How do I find the domain of a function given by an equation?
A: Identify any restrictions on the input values (x) that would make the function undefined, such as division by zero or taking the square root of a negative number. The domain is all real numbers except those restricted values.