CORRESPONDING ANGLES
Definition Of Corresponding Angles
Corresponding Angles are two congruent angles, both lying on the same side of the transversal and situated the same way on two different parallel lines.
More About Corresponding Angles
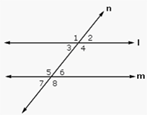
In the figure shown, l and m are two parallel lines cut by the transversal n. Angles 2 & 6, 4 & 8, 1 & 5, and 3 & 7 are corresponding angles.
Video Examples: Corresponding Angles
Solved Example on Corresponding Angles
Ques: How many pairs of corresponding angles are formed when two parallel lines are cut by a transversal?
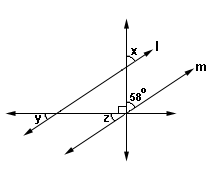
Choices:
A. 4
B. 6
C. 8
D. 2
Correct Answer: A
Solution:
Step 1: 4 pairs of corresponding angles are formed when two parallel lines are cut by a transversal.
Quick Summary
- Corresponding angles are formed when a transversal intersects two parallel lines.
- Corresponding angles are congruent (equal in measure).
⚠️ Common Mistakes
- Confusing corresponding angles with alternate interior or alternate exterior angles.
- Assuming angles are corresponding when the lines are not parallel.
🌍 Real-World Uses
- Construction: Ensuring parallel walls or beams in a building are aligned correctly using angle measurements.
- Navigation: Using angle measurements relative to a reference point (like North) to maintain a parallel course.
- Architecture: Designing symmetrical structures where corresponding angles must be equal for aesthetic and structural integrity.
📋 Standards Alignment
CCSS.MATH.CONTENT.8.G.A.5
🔗 Related Links
🍎 Teacher Insights
Use visual aids and hands-on activities to help students identify corresponding angles. Emphasize the importance of parallel lines for the congruence of corresponding angles.🎓 Prerequisites
- Parallel lines
- Transversal
- Angles
- Congruence
Check Your Knowledge
Q1: If two parallel lines are cut by a transversal, how many pairs of corresponding angles are formed?
Q2: Which of the following angle pairs are corresponding angles?
Frequently Asked Questions
Q: How can I identify corresponding angles?
A: Look for angles that are in the same relative position at each intersection of the transversal and the parallel lines. They should both be on the same side of the transversal and either both above or both below the parallel lines.
Q: Are corresponding angles always congruent?
A: Corresponding angles are congruent only if the two lines intersected by the transversal are parallel. If the lines are not parallel, the corresponding angles are not necessarily congruent.