POSTULATE

Postulate

Definition Of Postulate

Postulate is a true statement, which does not require to be proved.

Example of Postulate

example of Postulate

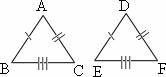
To prove that these triangles are congruent, we use SSS postulate, as the corresponding sides of both the triangles are equal.

Video Examples: The five postulates of Euclidean Geometry

Solved Example on Postulate

Ques: State the postulate or theorem you would use to prove that ∠1 and ∠2 are congruent.

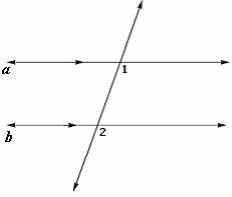
example of Postulate

Choices:

A. corresponding angles postulate
B. converse of corresponding angles postulate
C. alternate angles are congruent
D. adjacent angles are congruent

Correct Answer: A

Solution:

Step 1: ∠1 and ∠2 corresponding angles.
Step 2: Since the lines a and b are parallel, ∠1 and ∠2 are congruent. [Corresponding angles postulate.]
Step 3: So, corresponding angles postulate is used to prove that ∠1 and ∠2 are congruent.

Quick Summary

Postulates are true statements that do not require proof.
They are also called axioms.
Postulates are used to derive other logical statements.
The SSS postulate is used to prove triangle congruence.

\[ null \]

⚠️ Common Mistakes

Confusing postulates with theorems (theorems require proof).
Assuming a statement is a postulate without proper justification.

🌍 Real-World Uses

Architecture: Using geometric postulates to ensure the stability and accuracy of building designs.
Navigation: Applying postulates about lines and angles in GPS systems and mapmaking for accurate positioning.
Computer Graphics: Utilizing geometric postulates in rendering 3D models and creating realistic visual effects.

📋 Standards Alignment

CCSS.MATH.CONTENT.HSG.CO.A.1
CCSS.MATH.CONTENT.HSG.CO.B.7
CCSS.MATH.CONTENT.HSG.CO.C.10

🍎 Teacher Insights

Emphasize the difference between postulates and theorems. Use visual aids and real-world examples to illustrate the application of different postulates. Encourage students to question the validity of statements and determine whether they require proof or can be accepted as postulates.

🎓 Prerequisites

Basic geometric shapes
Understanding of logical statements
Concept of congruence

Check Your Knowledge

Q1: Which of the following is a postulate?

A. The sum of angles in a triangle is 180 degrees. B. Corresponding angles are congruent when lines are parallel. C. Vertical angles are congruent. D. The Pythagorean theorem.

Q2: What is another name for a postulate?

A. Theorem B. Axiom C. Corollary D. Lemma

Frequently Asked Questions

Q: What is the difference between a postulate and a theorem?
A: A postulate is assumed to be true without proof, while a theorem requires a proof based on previously established postulates or theorems.

Q: Are postulates universal, or can they vary?
A: While some postulates are universally accepted, different axiomatic systems can exist, each based on its own set of postulates. Euclidean Geometry is based on a set of postulates different from, for example, non-Euclidean geometries.