Solved Examples and Worksheet for Multiplying Polynomials

Q1What is the product of (y + 8) and (y + 4)?
A. y2 + 12y + 64
B. y2 + 12y + 32
C. y2 + 13y + 32
D. y2 + 11y + 32

Solutions
Share 
Step: 1
(y + 8)(y + 4)
  [Original expression.]
Step: 2
= y(y + 4) + 8(y + 4)
  [Distribute (y + 4) to each term of (y + 8).]
Step: 3
= y(y) + 4(y) + 8(y) + 8(4)
  [Distribute y and 8 to each term of (y + 4).]
Step: 4
= y2 + 4y + 8y + 32
  [Multiply.]
Step: 5
= y2 + 12y + 32
  [Combining like terms.]
Correct Answer is :   y2 + 12y + 32
Q2Find the number of terms that will be in the product when it is in simplest form.
(9y - 3) (9y - 3)
A. 2
B. 3
C. 1
D. 4

Solutions
Share 
Step: 1
(9y - 3) (9y - 3)
Step: 2
= (9y - 3)2
  [Perfect square.]
Step: 3
So, the product is a trinomial.
Correct Answer is :   3
Q3Find the number of terms that will be in the product when it is in the simplest form.
(8z + 8) (8z - 8)
A. 2
B. 4
C. 1
D. 3

Solutions
Share 
Step: 1
(8z + 8) (8z - 8)
Step: 2
The given expression is a product of two conjugate binomials, which is a special product with just two terms.
  [(a + b) (a - b) = a2 - b2.]
Correct Answer is :   2
Q4Find the number of terms that will be in the product when it is in the simplest form.
(w + x) (l + m)

A. 3
B. 2
C. 4
D. 1

Solutions
Share 
Step: 1
(w + x) (l + m)
Step: 2
The given expression is a product of two binomial factors, which are not identical. So, the product will be a polynomial of four terms.
Correct Answer is :   4
Q5Find the number of terms that will be in the product when it is in the simplest form. (2x - 5) (8x + 2)

A. 3
B. 1
C. 4
D. 2

Solutions
Share 
Step: 1
(2x - 5) (8x + 2)
Step: 2
The given expression is a product of two binomial factors, which are identical. So, the product is a trinomial.
Correct Answer is :   3
Q6Evaluate: (y + a) (y - a) (y2 + a2)
A. y4 - a4
B. y2 - a2
C. - y4 - a4
D. y4 + a4

Solutions
Share 
Step: 1
(y + a) (y - a) (y2 + a2)
Step: 2
= (y2 - a2) (y2 + a2)
  [Using special product: (y + a) (y - a) = y2 - a2.]
Step: 3
= (y2)2 -(a2)2
  [Using special product: (y + a) (y - a) = y2 - a2.]
Step: 4
= y4 - a4
  [Simplify.]
Correct Answer is :   y4 - a4
Q7What is the product of (y + 7) and (y + 10)?
A. y2 + 17y + 70
B. y2 + 70
C. y2 + 17y + 17
D. y2 + 7y + 70

Solutions
Share 
Step: 1
(y + 7)(y + 10)
  [Original expression.]
Step: 2
= y2 + 7y + 10y + 70
  [Use FOIL.]
Step: 3
= y2 + 17y + 70
  [Combining like terms.]
Correct Answer is :   y2 + 17y + 70
Q8What is the product of (y + 9) and (y + 5)?

A. y2 + 13y + 45
B. y2 + 14y + 45
C. y2 + 15y + 45
D. y2 + 14y + 90

Solutions
Share 
Step: 1
(y + 9)(y + 5)
  
Step: 2
= y(y + 5) + 9(y + 5)
  [Distribute (y + 5) to each term of (y + 9).]
Step: 3
= y(y) + 5(y) + 9(y) + 9(5)
  [Distribute y and 9 to each term of (y + 5).]
Step: 4
= y2 + 5y + 9y + 45
  [Multiply.]
Step: 5
= y2 + 14y + 45
  [Group the like terms.]
Correct Answer is :   y2 + 14y + 45
Q9Multiply (4u + 9v) with (2u + 5v).
A. 8u2 - 20uv + 45v2
B. 4u2 - 18uv - 45v2
C. 8u2 + 38uv + 45v2
D. 4u2 + 18uv + 45v2

Solutions
Share 
Step: 1
FOIL method to solve this problem.
Step: 2
That is, we multiply the first terms, then the outer terms, then the inner terms, and finally the last terms.
  [F-First, O-Outer, I-Inner, L-Last]
Step: 3

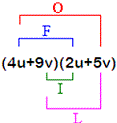
Step: 4
(4u)(2u) + (4u)(5v) + (9v)(2u) + (9v)(5v)
Step: 5
= 8u2 + 20uv + 18uv + 45v2
  [Multiply.]
Step: 6
8u2 + 38 uv + 45v2
  [Group the like terms.]
Correct Answer is :   8u2 + 38uv + 45v2
Q10Multiply: (5x - 2) (5x - 2)
A. 5x2 + 10x + 4
B. 25x2 + 20x + 4
C. 5x2 - 10x - 4
D. 25x2 - 20x + 4

Solutions
Share 
Step: 1
Use FOIL method to solve this problem. That is, we multiply the first terms, then the outer terms, then the inner terms, and finally the last terns.
  [F-First, O-Outer, I-Inner, L-Last]
Step: 2

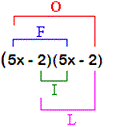
Step: 3
(5x)(5x) + (5x)( - 2) + ( - 2)(5x) + ( - 2)( - 2)
Step: 4
25x2 - 10 x - 10x + 4
  [Multiply.]
Step: 5
25x2 - 20x + 4
  [Group the like terms.]
Correct Answer is :   25x2 - 20x + 4
Q11Multiply (p - 4) and (p - 7).

A. p2 + 11p - 28
B. p2 - 4p - 11
C. p2 - 4p + 11
D. p2 - 11p + 28

Solutions
Share 
Step: 1
Use FOIL method to solve this problem.
That is, we multiply the first terms, then the outer terms, then the inner terms, and finally the last terms.
  [F-First, O-Outer, I-Inner, L-Last]
Step: 2

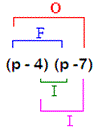
Step: 3
p(p) + p (-7) + (- 4)(p) + (-4)(- 7)
Step: 4
p2 - 7p - 4p + 28
  [Multiply.]
Step: 5
p2 - 11p + 28
  [Group the like terms.]
Correct Answer is :   p2 - 11p + 28
Q12Find: (n+ 6)(-n+6).
A. n2 + 6
B. - n2 + 36
C. n2 + 12n + 36
D. 4n2 + 6n + 16

Solutions
Share 
Step: 1
Use FOIL method to solve this problem.
That is, we multiply the first terms, then the outer terms, then the inner terms, and finally the last terns.
  [F-First, O-Outer, I-Inner, L-Last]
Step: 2

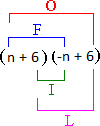
Step: 3
= (n)(-n) + (n)(6) + (-n)(6) + (6)(6)
  [Multiply.]
Step: 4
= - n2 + 6n - 6n + 36
Step: 5
- n2 + 36
Correct Answer is :   - n2 + 36

HighSchool Math