Solved Examples and Worksheet for Explicit and Recursive Formula in Contextual Problems
A.
B.
C.
D.
Step: 1
[First time.]
Step: 2
Step: 3
Step: 4
Step: 5
[Observe the pattern.]
Step: 6
Step: 7
The recursive formula is a a n
Correct Answer is : a a n
A.
B.
C.
D.
Step: 1
[First time.]
Step: 2
Step: 3
Step: 4
[Observe the pattern.]
Step: 5
Step: 6
The explicit formula is a n n n
Correct Answer is : a n n n
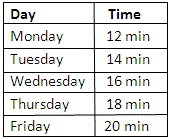
A.
B.
C.
D.
Step: 1
[First term.]
Step: 2
Step: 3
Step: 4
Step: 5
[Observe the pattern.]
Step: 6
[Explicit formula.]
Step: 7
An explicit formula ia a n
Step: 8
[First time.]
Step: 9
Step: 10
Step: 11
Step: 12
[Observe the pattern.]
Step: 13
[Recursive formula.]
Step: 14
The recursive formula is a a n
Correct Answer is : a n a a n
A.
B.
C.
D.
Step: 1
[Pencils bought by 1st friend.]
Step: 2
[Pencils bought by 2nd friend.]
Step: 3
[Pencils bought by 3rd friend.]
Step: 4
[By observing the pattern.]
Step: 5
An explicit formula is a n
Step: 6
Step: 7
The number of pencils bought by Candy's 4th friend are 64.
Correct Answer is : a n
A.
B.
C.
D.
Step: 1
Explicit formula
Step: 2
[First term.]
Step: 3
Step: 4
Step: 5
Step: 6
[Observe the pattern.]
Step: 7
Step: 8
Recursive formula
Step: 9
[First term.]
Step: 10
Step: 11
Step: 12
Step: 13
[Observe the pattern.]
Step: 14
[Observe the pattern.]
Step: 15
An explicit formula ia a n
Step: 16
The recursive formula is a a
Correct Answer is : a n a a n n
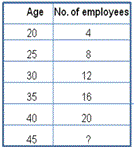
A.
B.
C.
D.
Step: 1
[Take No of employees at the age of 20 as first term.]
Step: 2
Step: 3
Step: 4
Step: 5
[Observe the pattern.]
Step: 6
Step: 7
The explicit formula is an = 4n
Step: 8
The number of employees at the age of 45 is a
[Substitute the value.]
Correct Answer is : a n
A.
B.
C.
D.
Step: 1
[Take the number of students in the 1st bus as first term.]
Step: 2
Step: 3
Step: 4
[Observe the sequence.]
Step: 5
[Observe the sequence.]
Step: 6
The recursive formula is a a
Correct Answer is : a a n
A.
B.
C.
D.
Step: 1
[First term.]
Step: 2
Step: 3
Step: 4
[Observe the pattern.]
Step: 5
Step: 6
The explicit formula is a n
Correct Answer is : a n
A.
B.
C.
D.
Step: 1
[First term.]
Step: 2
Step: 3
Step: 4
[Observe the pattern.]
Step: 5
Step: 6
The explicit formula is a n
Correct Answer is : a n
A.
B.
C.
D.
Step: 1
[First term.]
Step: 2
Step: 3
Step: 4
[Observe the pattern.]
Step: 5
Step: 6
The recursive formula is a a n
Correct Answer is : a a n
- Finding the Rule of a Function Table-Algebra1-Solved Examples
- Operations with Functions-Algebra1-Solved Examples
- Finding the Inverse of a Functions-Algebra1-Solved Examples
- Finding Even or Odd Functions-Algebra1-Solved Examples
Related Worksheet
- Recursive Formula