SECTOR
Definition Of Sector
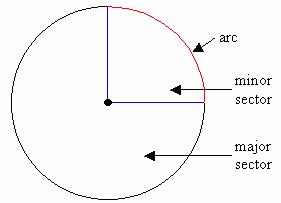
The area between an arc and two radii of a circle is called Sector.
More About Sector
Sector can also be referred as Wedge.
Asector is the region enclosed by two radii and an arc. The two radii divide the circle into two sectors called a major sector and a minor sector.
A minor sector has an angle at the centre of the circle of less than 180°.
A major sector has an angle at the centre of the circle of more than 180°.
Area of the sector of a circle of radius r is given as 1/2 r2θ.
Video Examples: Sectors and Cones - GCSE Maths Revision
Example of Sector
Solved Example on Sector
Ques: Find the area of the sector AOB.
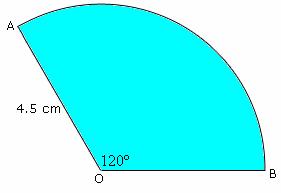
Choices:
A. 3.25p cm2
B. 4.5 cm2
C. 6.75p cm2
D. 3p cm2
Correct Answer: C
Solution:
Step 1: Area of the sector of a circle = 1/5r2? [Formula.]
Step 2: θ = 120° = 120 × π / 180 = 2π/3 radians [Convert degrees to radians.]
Step 3: = 1/2 × (4.5)2 × 2π/3 [Substitute the values.]
Step 4: = 6.75π [Simplify.]
Step 5: So, the area of the given sector is 6.75π cm2
Quick Summary
- A sector is a wedge-shaped part of a circle.
- A circle is divided into a major and minor sector.
- The area of a sector depends on the radius and the central angle.
🍎 Teacher Insights
Use visual aids and real-world examples like pizza slices to illustrate the concept of a sector. Emphasize the importance of using radians when applying the area formula.🎓 Prerequisites
- Area of a circle
- Radius
- Arc
- Radian measure
Check Your Knowledge
Q1: What is the area of a sector with radius 6 cm and central angle of π/3 radians?
Q2: A sector has an area of 25π and radius of 10. What is the angle of the sector?
Frequently Asked Questions
Q: What is the difference between a major and minor sector?
A: A minor sector has a central angle less than 180 degrees, while a major sector has a central angle greater than 180 degrees.
Q: How do you convert degrees to radians?
A: Multiply the degree measure by π/180.