HYPERBOLA

Hyperbola

Definition Of Hyperbola

Hyperbola is a conic section in which difference of distances of all the points from two fixed points (called `foci`) is constant.

More About Hyperbola

The general equation for hyperbola is .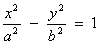
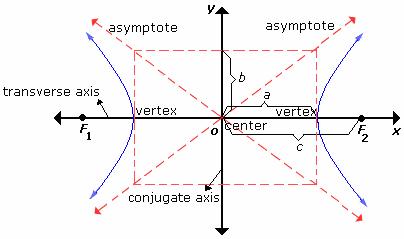
The eccentricity (e) of a hyperbola is always greater than 1, e > 1.
The slope of asymptotes for both horizontal and vertical hyperbola is .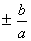

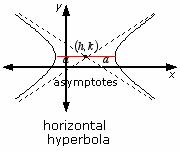
The equation for the horizontal hyperbola is .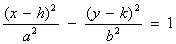

Video Examples: Hyperbola

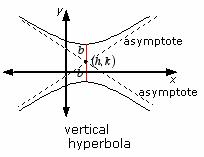
The equation for the vertical hyperbola is .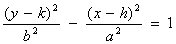
The foci of the hyperbola are (± ; c, 0).

Example of Hyperbola

Solved Example on Hyperbola

Ques: Choose the standard form of the equation for the hyperbola shown.

Choices:

Correct Answer: D

Solution:

Step 1: In the graph, 2c = 6 and 2a = 4 or c = 3, a = 2.
Step 2: c² = a² + b² [Pythagorean relation.]
Step 3: 9 = 4 + b² [Substitute 3 for c, 2 for a.]
Step 4: b² = 5
Step 5: Since the transverse axis is horizontal, the standard form of the hyperbola is 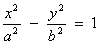or.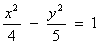

Quick Summary

Hyperbola is defined by the difference of distances from two foci being constant.
The general equation involves x^2 and y^2 terms with opposite signs.
Eccentricity (e) is always greater than 1.

\[ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \]

⚠️ Common Mistakes

Confusing the hyperbola equation with that of an ellipse.
Incorrectly identifying the center, vertices, and foci.
Forgetting to consider both positive and negative branches of the hyperbola.

🌍 Real-World Uses

Design of cooling towers in nuclear power plants which often have hyperbolic cross-sections for structural integrity and efficient airflow.
Trajectory calculations for long-range artillery or spacecraft, where the path may be hyperbolic depending on initial velocity and gravitational forces.
Certain lenses in telescopes use hyperbolic shapes to correct for aberrations and improve image quality.

📋 Standards Alignment

CCSS.MATH.HSG.GPE.A.3
CCSS.MATH.HSG.GPE.A.2

🍎 Teacher Insights

Emphasize the difference between hyperbola and ellipse equations. Use visual aids and real-world examples to illustrate the concept of constant difference of distances. Encourage students to practice graphing hyperbolas from different forms of the equation.

🎓 Prerequisites

Algebra
Coordinate Geometry
Conic Sections Basics

Check Your Knowledge

Q1: What is the standard form equation of a hyperbola with a horizontal transverse axis, centered at the origin?

x^2/a^2 + y^2/b^2 = 1 x^2/a^2 - y^2/b^2 = 1 y^2/a^2 - x^2/b^2 = 1 Ax^2 + By^2 + Cx + Dy + E = 0

Frequently Asked Questions

Q: What is the eccentricity of a hyperbola?
A: The eccentricity (e) of a hyperbola is always greater than 1 (e > 1).

Q: How do you find the asymptotes of a hyperbola?
A: The slope of the asymptotes for both horizontal and vertical hyperbolas can be found using the formula ±(b/a).