PERPENDICULAR BISECTOR
Definition Of Perpendicular Bisector
Perpendicular Bisector is a perpendicular line or a segment that passes through the midpoint of a line.
More About Perpendicular Bisector
A perpendicular bisector divides a line segment into two equal segments.
The intersecting point of the three perpendicular bisectors of a triangle is called circumcenter.
Examples of Perpendicular Bisector
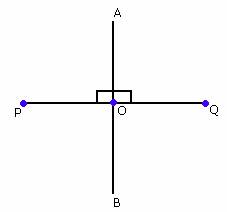
In the figure shown, AB is the perpendicular bisector of the line segment PQ passing through its midpoint 'O'.
Video Examples: Perpendicular Bisector of a Triangle - MathHelp.com
Solved Example on Perpendicular Bisector
Ques: AB is a line segment of length 12 cm. CD is the perpendicular bisector of AB. Find the length of AO and OB.
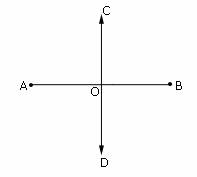
Choices:
A. 6 cm and 8 cm
B. 7 cm and 7 cm
C. 6 cm and 6 cm
D. 7 cm and 6 cm
Correct Answer: C
Solution:
Step 1: A perpendicular bisector divides a line segment into two equal parts.
Step 2: The length of AB is 12 cm and CD is the perpendicular bisector of AB.
Step 3: So, AO = OB =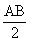 
= 
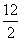= 6 [Substitute AB = 12.]
Step 4: AO = OB = 6 cm
Quick Summary
- A perpendicular bisector divides a line segment into two equal segments.
- It intersects the line segment at a 90-degree angle.
- The point of intersection is the midpoint of the original line segment.
- The circumcenter of a triangle is the intersection of the three perpendicular bisectors of the triangle's sides.
⚠️ Common Mistakes
- Confusing perpendicular bisectors with angle bisectors.
- Assuming any line that intersects a segment at a 90-degree angle is a perpendicular bisector (it must also pass through the midpoint).
- Thinking that a perpendicular bisector has to extend infinitely; it can be a line segment.
🌍 Real-World Uses
- Architecture: Ensuring walls are perpendicular and bisecting spaces for symmetrical room design.
- Construction: Building bridges where support beams must be perpendicular to the road surface and bisect the distance between support points.
- Navigation: Determining the shortest path between two points on a map by finding the perpendicular bisector of the line segment connecting them.
📋 Standards Alignment
CCSS.MATH.CONTENT.HSG.CO.C.9CCSS.MATH.CONTENT.HSG.CO.D.12
🔗 Related Links
🍎 Teacher Insights
Use physical manipulatives, such as rulers and protractors, to demonstrate the concept. Have students construct perpendicular bisectors using compass and straightedge. Emphasize the 'perpendicular' and 'bisector' parts of the term.🎓 Prerequisites
- Lines and Angles
- Line Segments
- Midpoint
- Perpendicular Lines
Check Your Knowledge
Q1: Which of the following statements is true about a perpendicular bisector of a line segment?
Q2: If point P lies on the perpendicular bisector of segment AB, then:
Frequently Asked Questions
Q: How do you construct a perpendicular bisector?
A: Using a compass, draw arcs from each endpoint of the line segment with a radius greater than half the segment's length. The line connecting the points where the arcs intersect is the perpendicular bisector.
Q: What is the relationship between a perpendicular bisector and the endpoints of the line segment it bisects?
A: Any point on the perpendicular bisector is equidistant from the two endpoints of the line segment.